��Ŀ����
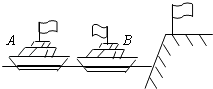
����Ŀ����·����һ������������10m/s���ٶ�����������ʻ�����ڳ����Ϊ25m��������һ��Ħ�г���20m/s���ٶ�ͬ����ʻ���������복�����һ����25mʱɲ������0.5m/s2�ļ��ٶ����ȼ����˶���Ħ�г��ڳ����Ա���ʻ�������賵�ӳ�����N�㹻�࣬��
��1��Ħ�г�����뼸������������Ħ�г�����복���������������Σ�
��2��Ħ�г��Ӹ��ϳ��ӵ��뿪���ӣ��������ʱ�䣿
���𰸡�
��1��
�⣺��Ħ�г��ٶȼ�Ϊ10m/sʱ������ʱΪt��Ħ�г���ʻ�ľ���Ϊx1��ÿ��������ʻ�ľ��붼Ϊx2��
v2=v1��at��
����ã�10=20��0.5t�����t=20s ��
![]() =��2ax1
=��2ax1
��ã�x1=300m ��
x2=v1t=200m ��
Ħ�г������һ�������ľ����x=300��200��25=75��m��
��Ħ�г��ϵ�������n= ![]() +1=4����
+1=4����
֮��������Ħ�г���Ħ�г������������Ĵ���Ϊ7��
��2��
�⣺��Ħ�г������һ��������ʱ��Ϊt1�����һ����������Ħ�г���ʱ��Ϊt2��
��x+v2t=v1t�� ![]()
��ã�t1=��20��10 ![]() ��s��t2=��20+10
��s��t2=��20+10 ![]() ��s
��s
��t=t2��t1=20 ![]() s
s
����������1����Ħ�г��ٶȼ�Ϊ10m/sʱ�����ٶȹ�ʽ���ʱ�䣬���ٶ�λ�ƹ�ʽ�ֱ�����˹���������Ħ�г���λ�ƣ��õ�Ħ�г������һ�������ľ��룬�������ڳ����Ϊ25m���Ħ�г������һ�������ľ�������������Ĵ�������2��Ħ�г������һ����������������ӵ�λ�������һ����������Ħ�г�λ��֮����Ħ�г��Ӹ��ϳ��ӵ��뿪���ӵ�ʱ�䣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ����ͼ���ѵ��ɲ����Ƶ�һ�˹̶���ǽ�ϣ�����Fˮƽ�����������壬�����������˶�����ʱ�����Ƶ�ʾ���ȶ���ͼ���Ѱѵ��ɲ����Ƶ�ʾ���Ŵ����������P��������Ļ���Ħ�����Ĵ�С�� N������Ϊ �� ���ɲ����Ʋ�����P��13N�����ݱ��и����Ķ�Ħ������������������P�IJ���Ϊ �� 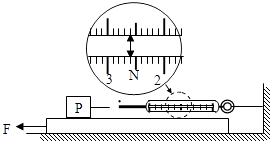
���� | ��Ħ������ |
���������� | 0.25 |
������ | 0.30 |
ľͷ������ | 0.20 |
Ƥ�敏���� | 0.28 |