题目内容
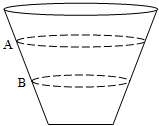如图所示，摩托车驾驶员在漏斗形筒壁上做飞车走壁表演，分别在A点和B点的高度绕不同的半径在水平方向上作匀速圆周运动．设在A、B点的速度分别为vA、vB，则（ ）分析：任选一摩托车作为研究对象，根据匀速圆周运动的合力提供向心力的特点，分析受力情况，作出力图，根据牛顿第二定律得到线速度与半径的关系，可比较它们的大小．
解答：解：A、以任摩托车为研究对象，作出力图，如图．设侧壁与竖直方向的夹角为θ，
则根据牛顿第二定律，
得mgcotθ=m
解得v=
r大，则v大，则在A轨道上运动时线速度较大，即vA＞vB．故A正确．
故选A．
则根据牛顿第二定律，
得mgcotθ=m
| v2 |
| r |
解得v=
| grcotθ |
r大，则v大，则在A轨道上运动时线速度较大，即vA＞vB．故A正确．
故选A．
点评：本题是圆维摆类型，支持力和重力的合力提供物体的向心力．对于几个相似情况的比较，往往以任意情况情况为例研究，得到一般的公式，然后比较大小．
练习册系列答案
相关题目
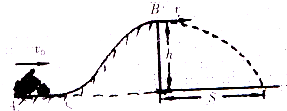（2004?潍坊模拟）如图所示，运动员驾驶摩托车做腾跃特技表演．运动员从斜坡底部的A处，以v0=l0m/s的初速度保持摩托车以额定功率P0=1.8kW行驶．经t=13s的时间冲上斜坡，然后从斜坡顶部已知人和车的总质量m=180kg，坡顶高度h=5m，落地点距B点的水平距离s=16m，不计空气阻力，重力加速度g=l0m/s2． 求：摩托车在冲上坡顶的过程中克服摩擦阻力做的功．
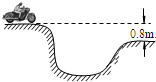如图所示，运动员驾驶摩托车跨越壕沟，壕沟两侧的高度差为0.8m．假设运动员跨越前沿水平路面行驶，则运动员跨过壕沟时在空中飞行的时间为（取g=10m/s2）（ ）
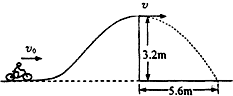如图所示，人驾驶摩托车做腾跃特技表演，以10m/s的初速度沿曲面冲上高3.2m顶部水平的高台，然后从高台水平飞出，落地点到飞出点的水平距离为5.6m、若摩托车冲上高台的过程中始终以额定功率1.8kW行驶，经过时间t到达顶部水平平台，已知人和车的总质量为180kg，特技表演的全过程中不计一切阻力，求时间t？（g=l0m/s2）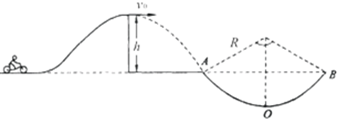
的水平速度冲出，落至地面时，恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道，并沿轨道下滑．A、B为圆弧两端点，其连线水平。已知圆弧半径为R=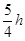
，人和车的总质量为m，特技表演的全过程中不计一切阻力，
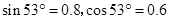。g为重力加速度。求：人和车运动到圆弧轨道最低点O时车对轨道的压力。