题目内容
9.宇航员在地球表面,以一定初速度竖直上抛一小球,测得小球从抛出到返回的时间为t;若他在某星球表面以相同的初速度竖直上抛同一小球,小球从抛出到返回时间为25t.若已知该星球的半径与地球半径之比为R2:R1=1:4,空气阻力不计.则( )| A. | 该星球表面的重力加速度与地球表面重力加速度之比为25:1 | |
| B. | 该星球的密度与地球密度之比为4:25 | |
| C. | 该星球与地球第一宇宙速度之比为10:1 | |
| D. | 在该星球与地球上自相同高度处以相同初速度平抛物体的水平射程之比为25:1 |
分析 由竖直上抛可以得到地球和星球表面重力加速度之比;
由万有引力提供向心力可得质量,进而可比较密度;
重力提供向心力,速度为第一宇宙速度;
由平抛运动规律可得水平射程之比.
解答 解:A、竖直上抛具有对称性,上下时间相等,故可得:v0=g•$\frac{t}{2}$,故星球表面重力加速度和地球表面重力加速度之比为g′:g=1:25,故A错误.
B、由mg=G$\frac{Mm}{{R}^{2}}$,解得:M=$\frac{g{R}^{2}}{G}$,密度为:ρ=$\frac{M}{V}$=$\frac{\frac{g{R}^{2}}{G}}{\frac{4}{3}π{R}^{3}}$=$\frac{3g}{4πGR}$,故密度之比为:ρ2:ρ1=$\frac{g′}{{R}_{2}}:\frac{g}{{R}_{1}}$=4:25,故B正确.
C、重力提供向心力,速度为第一宇宙速度,可得:mg=m$\frac{{v}^{2}}{R}$,解得:v=$\sqrt{gR}$,故该星球与地球第一宇宙速度之比为$\sqrt{1×1}$:$\sqrt{25×4}$=1:10,故C错误.
D、由平抛规律可得:
x=v0t,
h=$\frac{1}{2}$gt2,
解得:
x=v0$\sqrt{\frac{2h}{g}}$.
故在该星球与地球上自相同高度处以相同初速度平抛物体的水平射程之比:
x′:x=$\sqrt{\frac{1}{g′}}$:$\sqrt{\frac{1}{g}}$=$\sqrt{\frac{1}{25}}$:$\sqrt{\frac{1}{1}}$=1:5.
故D错误.
故选:B
点评 利用好星球上的竖直上抛或平抛运动是解决星球重力加速度的常用手段,结合万有引力提供向心力可解决问题.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案| A. | 速度 | B. | 动能 | ||
| C. | 质量和速度的乘积 | D. | 以上都不对 |
| A. | 在最高点速度为零,加速度也为零 | |
| B. | 上升某一高度和下落下降到此高度时的位移不相同 | |
| C. | 从上升到下降的整个过程中加速度保持不变 | |
| D. | 上升到某一高度时速度与下降到此高度时的速度相同 |
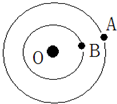 如图所示,两颗人造地球卫星A、B绕地心O做匀速圆周运动,已知A为同步卫星,B为近地卫星.则正确的判断是( )
如图所示,两颗人造地球卫星A、B绕地心O做匀速圆周运动,已知A为同步卫星,B为近地卫星.则正确的判断是( )| A. | 角速度大小的关系是ωA>ωB | |
| B. | 卫星A的周期为24小时小于卫星B的周期 | |
| C. | 向心加速度大小的关系是aA<aB | |
| D. | 卫星B的线速度大小为第一宇宙速度且小于卫星A的速度 |
| A. | 一个力可能有两个施力物体 | |
| B. | 重力没有施力物体 | |
| C. | 物体受到力的作用,其运动状态未必改变 | |
| D. | 压力就是重力 |
| A. | ${N_A}=\frac{V_0}{V_m}$ | B. | ${N_A}=\frac{V_m}{V_0}$ | C. | ${V_m}=\frac{M}{ρ}$ | D. | $m=\frac{M}{N_A}$ |
| A. | 一对相互作用力做功的代数和必为零 | |
| B. | 合外力做负功时,物体的机械能可能不变 | |
| C. | 摩擦力只能对物体做负功从而使物体动能减小 | |
| D. | 物体的重力势能从-8J变为-3J,重力势能减少了5J |
 如图所示,圆盘在水平面内匀速转动,放置于圆盘上的小物体相对于圆盘静止,下列关于小物体所受力的分析正确的是( )
如图所示,圆盘在水平面内匀速转动,放置于圆盘上的小物体相对于圆盘静止,下列关于小物体所受力的分析正确的是( )| A. | 重力和支持力 | B. | 重力、支持力和向心力 | ||
| C. | 重力、支持力和摩擦力 | D. | 重力、支持力和离心力 |