题目内容
16.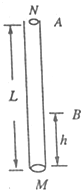 如图所示是研究带电体的质量与电量关系的光滑绝缘细管,长为L,竖直放置,点电荷M固定子啊管底部,电荷量为+Q,现在从管口A处由静止释放一电荷量为+q、质量为m的带电体N,当其下部落至距M为h的B处时速度恰好为0,已知静电力常量为k,重力加速度为g,带电体下落过程中不影响原电场
如图所示是研究带电体的质量与电量关系的光滑绝缘细管,长为L,竖直放置,点电荷M固定子啊管底部,电荷量为+Q,现在从管口A处由静止释放一电荷量为+q、质量为m的带电体N,当其下部落至距M为h的B处时速度恰好为0,已知静电力常量为k,重力加速度为g,带电体下落过程中不影响原电场(1)N在运动过程中速度最大处与M的距离
(2)若把N换成电荷量+q、质量为3m的带电体P,仍从A处由静止释放,求P到达B处时的速度大小.
分析 (1)电荷N运动到重力等于电场力时,速度最大,根据平衡条件和库仑定律求解速度最大处与M的距离.
(2)对两个粒子,分别根据动能定理列式即可求解.
解答 解:(1)电荷N运动到重力等于电场力时,速度最大,设此时距底部M的距离为r,则有
mg=k$\frac{Qq}{{r}^{2}}$
解得:r=$\sqrt{\frac{kQq}{mg}}$
(2)设电荷P运动到B处时的速度为vB,由动能定理,有
3mg(L-h)+qUAB=$\frac{1}{2}•$3m${v}_{B}^{2}$
带电体N由A到B过程中,有:mg(L-h)+qUAB=0
联立两式可得:vB=2$\sqrt{\frac{g(L-h)}{3}}$.
答:
(1)N在运动过程中速度最大处与M的距离是$\sqrt{\frac{kQq}{mg}}$.
(2)P到达B处时的速度大小为2$\sqrt{\frac{g(L-h)}{3}}$.
点评 本题综合考查动力学知识及库仑力公式的应用,解题的关键在于明确物体的运动过程,运用动能定理列式研究.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
6.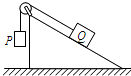 如图所示,表面粗糙的固定斜面顶端安有定滑轮,两物块P、Q用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦),P悬于空中,Q放在斜面上,均处于静止状态.当用水平向左的恒力推Q时,P、Q仍静止不动,则( )
如图所示,表面粗糙的固定斜面顶端安有定滑轮,两物块P、Q用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦),P悬于空中,Q放在斜面上,均处于静止状态.当用水平向左的恒力推Q时,P、Q仍静止不动,则( )
 如图所示,表面粗糙的固定斜面顶端安有定滑轮,两物块P、Q用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦),P悬于空中,Q放在斜面上,均处于静止状态.当用水平向左的恒力推Q时,P、Q仍静止不动,则( )
如图所示,表面粗糙的固定斜面顶端安有定滑轮,两物块P、Q用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦),P悬于空中,Q放在斜面上,均处于静止状态.当用水平向左的恒力推Q时,P、Q仍静止不动,则( )| A. | 轻绳上拉力一定变小 | B. | 轻绳上拉力一定不变 | ||
| C. | Q受到的摩擦力一定变大 | D. | 斜面对Q的支持力一定变大 |
4. 如图所示,是按一定比例尺绘制的太阳系五颗行星的轨道,可以看出,行星的轨道十分接近圆,由图可知( )
如图所示,是按一定比例尺绘制的太阳系五颗行星的轨道,可以看出,行星的轨道十分接近圆,由图可知( )
 如图所示,是按一定比例尺绘制的太阳系五颗行星的轨道,可以看出,行星的轨道十分接近圆,由图可知( )
如图所示,是按一定比例尺绘制的太阳系五颗行星的轨道,可以看出,行星的轨道十分接近圆,由图可知( )| A. | 火星的公转周期小于地球的公转周期 | |
| B. | 水星的公转速度小于地球的公转速度 | |
| C. | 木星的公转角速度小于地球的公转角速度 | |
| D. | 金星的向心加速度小于地球的向心加速度 |
1. 如图所示,在匀速转动的水平圆盘上,沿半径方向放着用细线相连的质量相等的两个物体A和B,它们与盘间的动摩擦因数相同,当圆盘转动到两个物体刚好还未发生滑动时,烧断细线后,两个物体的运动情况是( )
如图所示,在匀速转动的水平圆盘上,沿半径方向放着用细线相连的质量相等的两个物体A和B,它们与盘间的动摩擦因数相同,当圆盘转动到两个物体刚好还未发生滑动时,烧断细线后,两个物体的运动情况是( )
 如图所示,在匀速转动的水平圆盘上,沿半径方向放着用细线相连的质量相等的两个物体A和B,它们与盘间的动摩擦因数相同,当圆盘转动到两个物体刚好还未发生滑动时,烧断细线后,两个物体的运动情况是( )
如图所示,在匀速转动的水平圆盘上,沿半径方向放着用细线相连的质量相等的两个物体A和B,它们与盘间的动摩擦因数相同,当圆盘转动到两个物体刚好还未发生滑动时,烧断细线后,两个物体的运动情况是( )| A. | 两物体均沿切向方向滑动 | |
| B. | 物体B仍随圆盘一起做圆周运动,物体A发生滑动 | |
| C. | 两物体仍随圆盘一起做圆周运动,不发生滑动 | |
| D. | 两物体均沿半径方向滑动,离圆盘圆心越来越远 |
8.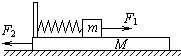 如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m、M及M与地面间摩擦不计.开始时,m和M均静止,现同时对m、M施加等大反方向的商品恒力F1和F2,设两物体开始运动以后的整个运动过程中,弹簧形变不超过器弹性限度.对于m、M和弹簧组成的系统( )
如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m、M及M与地面间摩擦不计.开始时,m和M均静止,现同时对m、M施加等大反方向的商品恒力F1和F2,设两物体开始运动以后的整个运动过程中,弹簧形变不超过器弹性限度.对于m、M和弹簧组成的系统( )
 如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m、M及M与地面间摩擦不计.开始时,m和M均静止,现同时对m、M施加等大反方向的商品恒力F1和F2,设两物体开始运动以后的整个运动过程中,弹簧形变不超过器弹性限度.对于m、M和弹簧组成的系统( )
如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m、M及M与地面间摩擦不计.开始时,m和M均静止,现同时对m、M施加等大反方向的商品恒力F1和F2,设两物体开始运动以后的整个运动过程中,弹簧形变不超过器弹性限度.对于m、M和弹簧组成的系统( )| A. | 由于F1、F2等大反向,故系统机械能守恒 | |
| B. | 运动过程中F1、F2可能做正功,也可能做负功 | |
| C. | 由于F1、F2大小不变,所以m、M各自已知做匀加速运动 | |
| D. | 当弹簧弹力大小与F1、F2大小相等时,m、M各自的动能最大 |
3.物理学家们的科学发现推动了物理学的发展、人类的进步.在对以下几位物理学家所作科学贡献的叙述中正确的是( )
| A. | 库仑发现了点电荷之间的相互作用规律 | |
| B. | 牛顿发现了弹力与物体形变量间的变化规律 | |
| C. | 奥斯特发现了磁场产生电流的条件和规律 | |
| D. | 伽利略提出的万有引力定律奠定了天体力学的基础 |
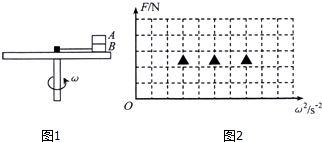
 探究力对原来静止的物体做功与物体获得的速度的关系的实验装置如图所示,实验主要过程如下:
探究力对原来静止的物体做功与物体获得的速度的关系的实验装置如图所示,实验主要过程如下: