题目内容
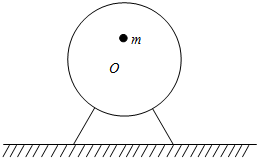如图是一种电动夯的结构为：在固定于夯上的电动机的转轴上固定一杆，杆的另一端固定一铁块，工作时电动机带动杆与铁块在竖直平面内匀速转动，则当铁块转至最低点时，夯对地面将产生很大的压力而夯实地面．设夯的总质量为M，铁块质量为m，杆的质量不计．电动机的转速可以调节，为了安全，夯在工作中不离开地面，则此夯能对地面产生的最大压力为多少？分析：铁块做圆周运动，在最高点靠重力和拉力的合力提供向心力，当拉力的大小等于电动机连同打夯机底座的重力时，才能使打夯机底座刚好离开地面．由牛顿第二定律求出此时铁块的速度，当铁块转至最低点时对地面产生的最大压力，再由牛顿第二定律求解．
解答：解：设杆长为L，由题意可知，当铁块转至最高点时，由牛顿第二定律得
F+mg=m
①
又由题意得F=（M-m）g ②
当铁块转至最低点时有
F′-mg=m
③
则夯对地面的最大压力为
N=（M-m）g+F′④
由①、②、③、④式解得 N=2Mg
答：夯在工作中不离开地面，则此夯能对地面产生的最大压力为2Mg．
F+mg=m
| v2 |
| L |
又由题意得F=（M-m）g ②
当铁块转至最低点时有
F′-mg=m
| v2 |
| L |
则夯对地面的最大压力为
N=（M-m）g+F′④
由①、②、③、④式解得 N=2Mg
答：夯在工作中不离开地面，则此夯能对地面产生的最大压力为2Mg．
点评：解决本题的关键采用隔离法分析，对铁块，在竖直方向上的合力提供圆周运动的向心力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
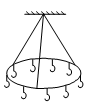如图是一种晾衣架的结构示意图，其结构是在质量均匀的圆环上对称的安装挂钩，三根等长的细线固定在圆环的三等分点上，细线上端连在一起固定在水平横梁上．已知每根细线长均为20cm，圆环半径为12cm，晾衣架的总重力为G，（不计细线重力），则每根细线所受拉力大小是（ ）
如图是一种升降电梯的示意图，A为载人箱，B为平衡重物，它们的质量均为M，上下均有跨过滑轮的钢索系住，在电动机的牵引下使电梯上下运动．如果电梯中乘客的质量为m，匀速上升的速度为v，电梯即将到顶层前关闭电依靠惯性上升h高度后停止，在不计空气和摩擦阻力的情况下，重力加速度为g，下列说法正确的是（ ）
如图是一种电动夯的结构为：在固定于夯上的电动机的转轴上固定一杆，杆的另一端固定一铁块，工作时电动机带动杆与铁块在竖直平面内匀速转动，则当铁块转至最低点时，夯对地面将产生很大的压力而夯实地面．设夯的总质量为M，铁块质量为m，杆的质量不计．电动机的转速可以调节，为了安全，夯在工作中不离开地面，则此夯能对地面产生的最大压力为多少？