题目内容
2.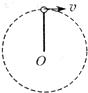 如图所示,轻杆一端与质量为1kg、可视为质点的小球相连,另一端可绕光滑固定轴在竖直平面内自由转动.现使小球在竖直平面内做圆周运动,经最高点时,小球速度大小为2m/s,且恰好对杆无作用力,g取10m/s2,不计空气阻力.下列说法中正确的是( )
如图所示,轻杆一端与质量为1kg、可视为质点的小球相连,另一端可绕光滑固定轴在竖直平面内自由转动.现使小球在竖直平面内做圆周运动,经最高点时,小球速度大小为2m/s,且恰好对杆无作用力,g取10m/s2,不计空气阻力.下列说法中正确的是( )| A. | 轻杆的长度为0.5m | B. | 轻杆的长度为1m | ||
| C. | 小球在最低点的速度大小为2$\sqrt{3}$m/s | D. | 小球在最低点的速度大小为2$\sqrt{5}$m/s |
分析 在最高点,且恰好对杆无作用力,由重力提供向心力,根据牛顿第二定律列式求解轻杆的长度,从最高点到最低点的过程中,根据动能定理求解小球在最低点的速度大小.
解答 解:A、在最高点,且恰好对杆无作用力,由重力提供向心力,根据牛顿第二定律得:
$mg=m\frac{{v}^{2}}{l}$
解得:l=$\frac{{v}^{2}}{g}=\frac{4}{10}=0.4m$,故AB错误;
C、从最高点到最低点的过程中,根据动能定理得:
$\frac{1}{2}mv{′}^{2}-\frac{1}{2}m{v}^{2}=mg•2l$
解得:v$′=2\sqrt{5}m/s$,故C错误,D正确.
故选:D
点评 该题考查竖直平面内的圆周运动,将牛顿第二定律与动能定理相结合即可正确解答,难度适中.

练习册系列答案
相关题目
12.下列关于时间和时刻的说法中,正确是( )
| A. | 时间和时刻的区别在于长短不同,长的是时间,短的是时刻 | |
| B. | 两个时刻之间的间隔是一段时间 | |
| C. | 第3秒末和第4秒初是同一时刻 | |
| D. | 第3秒内和第4秒内经历的时间不一样 |
13.${\;}_{92}^{238}$U经3次α衰变和2次β衰变后变为一个新核.这个新核的质子数为( )
| A. | 88 | B. | 84 | C. | 138 | D. | 226 |
10.n个共点力作用在一个质点上,使质点处于平衡状态,当其中的F1逐渐减小时,下列说法中正确的是( )
| A. | 物体仍然处于静止状态 | |
| B. | 物体的合力逐渐减小,与F1同向 | |
| C. | 物体的合力逐渐增大,与F1反向 | |
| D. | 当F1减小到零时,物体的合力大小为F1 |
17. 在如图所示的电路中,电源的负极接地,其电动势为E、内阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,
在如图所示的电路中,电源的负极接地,其电动势为E、内阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器, 、
、 为理想电流表和电压表.在滑动变阻器滑片P自a端向b端滑动的过程中,下列说法中正确的是( )
为理想电流表和电压表.在滑动变阻器滑片P自a端向b端滑动的过程中,下列说法中正确的是( )
 在如图所示的电路中,电源的负极接地,其电动势为E、内阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,
在如图所示的电路中,电源的负极接地,其电动势为E、内阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器, 、
、 为理想电流表和电压表.在滑动变阻器滑片P自a端向b端滑动的过程中,下列说法中正确的是( )
为理想电流表和电压表.在滑动变阻器滑片P自a端向b端滑动的过程中,下列说法中正确的是( )| A. | 电源的输出功率减小 | B. | 电流表的示数变大 | ||
| C. | a点的电势升高 | D. | 电容器C所带的电荷量增多 |
14.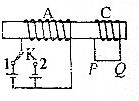 如图所示,C线圈闭合,A线圈与电池组成闭合回路,若把电键K从“1”拔向“2”,则跟线圈C相连的直导线PQ中的电流方向应是( )
如图所示,C线圈闭合,A线圈与电池组成闭合回路,若把电键K从“1”拔向“2”,则跟线圈C相连的直导线PQ中的电流方向应是( )
 如图所示,C线圈闭合,A线圈与电池组成闭合回路,若把电键K从“1”拔向“2”,则跟线圈C相连的直导线PQ中的电流方向应是( )
如图所示,C线圈闭合,A线圈与电池组成闭合回路,若把电键K从“1”拔向“2”,则跟线圈C相连的直导线PQ中的电流方向应是( )| A. | 始终是从P到Q | B. | 始终是从Q到P | ||
| C. | 先从P到Q,再从Q到P | D. | 先从Q到P,再从P到Q |
19.下列说法正确的是( )
| A. | 布朗运动时是固体微粒的运动,它说明液体分子水不停息地做无规则运动 | |
| B. | 在内径小的容器里,如果液体能浸润器壁,液面呈凸形 | |
| C. | 在保持体积不变的情况下,不断降低气体的温度,可以使未饱和汽变为饱和汽 | |
| D. | 单晶体的所有物理性质都是各向异性的. | |
| E. | 热量可以自发地从高温物体传到低温物体,但不断自发的从低温物体传递到高温物体 |
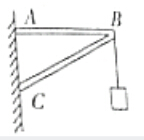 如图所示,在轻质的三角架上的B点细绳悬挂一个重为G的物体,则水平横梁受到的是拉力,斜梁BC受到的是压力作用.(填“拉”或“压”)
如图所示,在轻质的三角架上的B点细绳悬挂一个重为G的物体,则水平横梁受到的是拉力,斜梁BC受到的是压力作用.(填“拉”或“压”) 水平放置的平行金属板相距为d,板间有垂直纸面向里的匀强磁场,磁感应强度为B,极板按如图所示的方式接入电路.已知电源内阻为r,滑动变阻器的总阻值为R,滑片P的位置位于变阻器的中点.有一个质量为m、电荷量为+q的带电粒子,从两板中间左端沿中心线水平射入场区.不计粒子重力.
水平放置的平行金属板相距为d,板间有垂直纸面向里的匀强磁场,磁感应强度为B,极板按如图所示的方式接入电路.已知电源内阻为r,滑动变阻器的总阻值为R,滑片P的位置位于变阻器的中点.有一个质量为m、电荷量为+q的带电粒子,从两板中间左端沿中心线水平射入场区.不计粒子重力.