Question

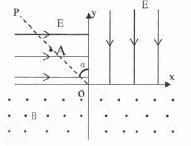
（2103浙江省六校联盟联考）在xoy平面内，直线OP与y轴的夹角=45^o。第一、第二象限内存在大小相等，方向分别为竖直向下和水平向右的匀强电场E；在x轴下方有垂直于纸面向外的匀强磁场B，如图所示。现有一带正电的粒子从直线OP上某点A（-L, L）处静止释放。设粒子的比荷，粒子重力不计，其中E、B、m、q均未知。求：

　 （1）粒子进入磁场时与x轴交点的横坐标。

　 （2）粒子进入磁场时速度方向与x轴正方向的夹角。

　 （3）如果在直线OP上各点释放许多个上述带电粒子（粒子间的相互作用力不计），试证明各带电粒子进入磁场后做圆周运动的圆心点的集合为一抛物线（提示：写出圆心点坐标x、y的函数关系）。

Answer 1

将B=代人上式得R=.

所以圆心坐标为：x=2L-R，y=-R。

将R=.代人并消去L得：x=4y²+y。

此方程为一抛物线方程。即各带电粒子进入磁场后做圆周运动的圆心点的集合为一抛物线。