题目内容
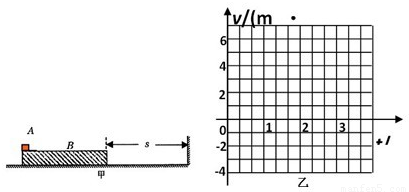
(本题只允许用牛顿运动定律求解)如图甲所示,一质量为M=2.0kg的长木板B静止于光滑水平面上,B的右边放有竖直挡板.小物体A(可视为质点)的质量均为m=1.0kg.t=0时刻对物体A施加瞬间冲量,使A以v=6.0m/s的初速度向右运动,已知A和B间的动摩擦因数μ=0.20,B与竖直挡板的碰撞时间极短,且碰撞时无机械能损失.重力加速度取g=10m/s2.(1)若A、B达到共同速度前并未碰到挡板,则B的右端距挡板的距离s至少多长?
(2)若B的右端距挡板距离s=0.50m,要使A在B碰到挡板前不脱离B,则木板B的长度至少多长?
(3)若木板B的长度L=9.0m,s=0.50m,取v方向为正,请在图乙的坐标纸上画出从t=0时刻起,A、B运动3.0s内的速度一时间图象(不要求书写计算过程,但要准确画出v━t图象).
【答案】分析:(1)A物体以一定的初速度向右运动,受到滑动摩擦力作用而做匀减速运动,B受到向右的滑动摩擦力而做匀加速运动,根据牛顿第二定律分别求出两个物体的加速度,由运动学公式求出速度相同时所用的时间,得到共同速度,再由运动学公式求出B运动的位移,即可得到B的右端距挡板的最小距离s;
(2)由B的位移公式求出时间,再位移公式求解A的位移,两者位移之差即为木板的长度.
(3)若木板B的长度L=9.0m,s=0.50m,根据两物体的运动情况,画出v-t图象.
解答:解:(1)A的加速度的大小为aA=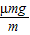 =μg=2m/s2,B的加速度的大小为aB=
=μg=2m/s2,B的加速度的大小为aB=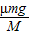 =1m/s2.
=1m/s2.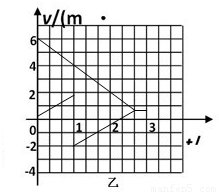
设两个物体达到共同速度所用的时间为t,则有:
v-aAt=aBt
解得:t=2s
此过程中B的位移为xB=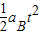 =2m.故B的右端距挡板的距离s至少2m.
=2m.故B的右端距挡板的距离s至少2m.
(2)若B的右端距挡板距离s=0.50m<2m,说明两个物体的速度还没有相同.
对于B,由s=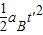 ,解得,t′=1s,
,解得,t′=1s,
此过程中,A的位移为xA=vAt′-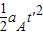 =5m
=5m
故要使A在B碰到挡板前不脱离B,木板B的长度至少为L=xA-xB=4.5m
(3)由上知,t=1s时B与挡板相撞,此后B向左做匀减速运动,A向右继续向右做匀减速运动,速度相同后一起向右运动.从t=0时刻起,A、B运动3.0s内的速度一时间图象如图.
答:(1)若A、B达到共同速度前并未碰到挡板,则B的右端距挡板的距离s至少2m.
(2)若B的右端距挡板距离s=0.50m,要使A在B碰到挡板前不脱离B,则木板B的长度至少4.5m.
(3)如图所示.
点评:本题通过计算要分析物体的运动情况,抓住两个物体之间位移关系、速度关系是关键.
(2)由B的位移公式求出时间,再位移公式求解A的位移,两者位移之差即为木板的长度.
(3)若木板B的长度L=9.0m,s=0.50m,根据两物体的运动情况,画出v-t图象.
解答:解:(1)A的加速度的大小为aA=
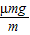 =μg=2m/s2,B的加速度的大小为aB=
=μg=2m/s2,B的加速度的大小为aB=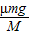 =1m/s2.
=1m/s2.
设两个物体达到共同速度所用的时间为t,则有:
v-aAt=aBt
解得:t=2s
此过程中B的位移为xB=
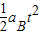 =2m.故B的右端距挡板的距离s至少2m.
=2m.故B的右端距挡板的距离s至少2m.(2)若B的右端距挡板距离s=0.50m<2m,说明两个物体的速度还没有相同.
对于B,由s=
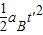 ,解得,t′=1s,
,解得,t′=1s,此过程中,A的位移为xA=vAt′-
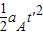 =5m
=5m故要使A在B碰到挡板前不脱离B,木板B的长度至少为L=xA-xB=4.5m
(3)由上知,t=1s时B与挡板相撞,此后B向左做匀减速运动,A向右继续向右做匀减速运动,速度相同后一起向右运动.从t=0时刻起,A、B运动3.0s内的速度一时间图象如图.
答:(1)若A、B达到共同速度前并未碰到挡板,则B的右端距挡板的距离s至少2m.
(2)若B的右端距挡板距离s=0.50m,要使A在B碰到挡板前不脱离B,则木板B的长度至少4.5m.
(3)如图所示.
点评:本题通过计算要分析物体的运动情况,抓住两个物体之间位移关系、速度关系是关键.

练习册系列答案
相关题目
 (本题只允许用牛顿运动定律求解)如图甲所示,一质量为M=2.0kg的长木板B静止于光滑水平面上,B的右边放有竖直挡板.小物体A(可视为质点)的质量均为m=1.0kg.t=0时刻对物体A施加瞬间冲量,使A以v0=6.0m/s的初速度向右运动,已知A和B间的动摩擦因数μ=0.20,B与竖直挡板的碰撞时间极短,且碰撞时无机械能损失.重力加速度取g=10m/s2.
(本题只允许用牛顿运动定律求解)如图甲所示,一质量为M=2.0kg的长木板B静止于光滑水平面上,B的右边放有竖直挡板.小物体A(可视为质点)的质量均为m=1.0kg.t=0时刻对物体A施加瞬间冲量,使A以v0=6.0m/s的初速度向右运动,已知A和B间的动摩擦因数μ=0.20,B与竖直挡板的碰撞时间极短,且碰撞时无机械能损失.重力加速度取g=10m/s2.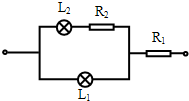 有两个小灯泡,它们的额定电压和额定功率分别是L1“3V、3W”和L2“2V、1.2W”.现把它们接在电压为6V的电源上,使两个小灯泡都能正常发光.在只允许用两个备用电阻的条件下,某同学设计出如图所示的电路.
有两个小灯泡,它们的额定电压和额定功率分别是L1“3V、3W”和L2“2V、1.2W”.现把它们接在电压为6V的电源上,使两个小灯泡都能正常发光.在只允许用两个备用电阻的条件下,某同学设计出如图所示的电路. (本题只允许用牛顿运动定律求解)如图甲所示,一质量为M=2.0kg的长木板B静止于光滑水平面上,B的右边放有竖直挡板.小物体A(可视为质点)的质量均为m=1.0kg.t=0时刻对物体A施加瞬间冲量,使A以v0=6.0m/s的初速度向右运动,已知A和B间的动摩擦因数μ=0.20,B与竖直挡板的碰撞时间极短,且碰撞时无机械能损失.重力加速度取g=10m/s2.
(本题只允许用牛顿运动定律求解)如图甲所示,一质量为M=2.0kg的长木板B静止于光滑水平面上,B的右边放有竖直挡板.小物体A(可视为质点)的质量均为m=1.0kg.t=0时刻对物体A施加瞬间冲量,使A以v0=6.0m/s的初速度向右运动,已知A和B间的动摩擦因数μ=0.20,B与竖直挡板的碰撞时间极短,且碰撞时无机械能损失.重力加速度取g=10m/s2.