题目内容
18.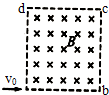 如图所示,边长为L的正方形区域abcd内存在着匀强磁场.一个质量为m、电荷量为q、初速度为υ0带电粒子从a点沿ab方向进人磁场,不计重力,则( )
如图所示,边长为L的正方形区域abcd内存在着匀强磁场.一个质量为m、电荷量为q、初速度为υ0带电粒子从a点沿ab方向进人磁场,不计重力,则( )| A. | 若粒子恰好从c点离开磁场,则磁感应强度B=$\frac{{m{υ_0}}}{2Lq}$ | |
| B. | 若粒子恰好从d点离开磁场,则磁感应强度B=$\frac{{m{υ_0}}}{Lq}$ | |
| C. | 若粒子恰好从bc边的中点离开磁场,则磁感应强度B=$\frac{{4m{υ_0}}}{5Lq}$ | |
| D. | 粒子从c点离开磁场时的动能大于从bc边的中点离开磁场时的动能 |
分析 粒子进入匀强磁场中做匀圆周运动,根据轨迹求出轨迹半径,再由半径公式求解B.
解答  解:A、若粒子恰好从c点离开磁场,轨迹半径 r=L,由r=$\frac{m{v}_{0}}{qB}$,得磁感应强度B=$\frac{m{v}_{0}}{Lq}$.故A错误.
解:A、若粒子恰好从c点离开磁场,轨迹半径 r=L,由r=$\frac{m{v}_{0}}{qB}$,得磁感应强度B=$\frac{m{v}_{0}}{Lq}$.故A错误.
B、若粒子恰好从d点离开磁场,轨迹半径 r=$\frac{1}{2}$L,由r=$\frac{m{v}_{0}}{qB}$,得磁感应强度B=$\frac{2m{v}_{0}}{Lq}$.故B错误.
C、若粒子恰好从bc边的中点离开磁场,其运动轨迹如图所示,由几何知识得:r2=(r-$\frac{L}{2}$)2+L2;可得 r=$\frac{5}{4}$L
由r=$\frac{m{v}_{0}}{qB}$,得磁感应强度 B=$\frac{{4m{υ_0}}}{5Lq}$.故C正确.
D、该题改变的是磁感应强度,粒子的入射速度是不变的,由于洛伦兹力不做功,不能改变粒子的动能,所以粒子从c点离开磁场时和从bc边的中点离开磁场时的动能相等.故D错误.
故选:C.
点评 解决本题的关键画出粒子的轨迹:定圆心,定半径,并要掌握带电粒子在磁场中做圆周运动的半径公式,结合几何关系求解.

练习册系列答案
相关题目
8.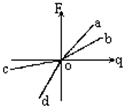 在一个电场中a、b、c、d四个点分别引入试探电荷时,电荷所受 到的电场力F跟引入电荷的电荷量之间的函数关系如图所示,下列说法中正确的是( )
在一个电场中a、b、c、d四个点分别引入试探电荷时,电荷所受 到的电场力F跟引入电荷的电荷量之间的函数关系如图所示,下列说法中正确的是( )
 在一个电场中a、b、c、d四个点分别引入试探电荷时,电荷所受 到的电场力F跟引入电荷的电荷量之间的函数关系如图所示,下列说法中正确的是( )
在一个电场中a、b、c、d四个点分别引入试探电荷时,电荷所受 到的电场力F跟引入电荷的电荷量之间的函数关系如图所示,下列说法中正确的是( )| A. | 这个电场是匀强电场 | |
| B. | a、b、c、d四点的电场强度大小关系是Ed>Ea>Eb>Ec | |
| C. | 同一点的电场强度随试探电荷电荷量的增加而增加 | |
| D. | 无法比较以上四点的电场强度值 |
6. 质量为m可视为质点的物体,在所受合外力F作用下运动的速度v随时间变化的规律如图所示,合外力的方向始终在一条直线上.已知t=0时质点的速度为零,在图示的t1、t2、t3和t4各时刻中,下列说法正确的是( )
质量为m可视为质点的物体,在所受合外力F作用下运动的速度v随时间变化的规律如图所示,合外力的方向始终在一条直线上.已知t=0时质点的速度为零,在图示的t1、t2、t3和t4各时刻中,下列说法正确的是( )
 质量为m可视为质点的物体,在所受合外力F作用下运动的速度v随时间变化的规律如图所示,合外力的方向始终在一条直线上.已知t=0时质点的速度为零,在图示的t1、t2、t3和t4各时刻中,下列说法正确的是( )
质量为m可视为质点的物体,在所受合外力F作用下运动的速度v随时间变化的规律如图所示,合外力的方向始终在一条直线上.已知t=0时质点的速度为零,在图示的t1、t2、t3和t4各时刻中,下列说法正确的是( )| A. | t1后物体运动的速度方向改变 | |
| B. | t1到t3时间内物体受到的合外力与选定的正方向相反 | |
| C. | t2时刻物体的速度为零、合外力也为零 | |
| D. | t2时刻物体又回到出发点 |
10.下列关于电场线的论述,正确的是( )
| A. | 电场线的切线方向就是正检验电荷在该点的受力方向 | |
| B. | 电场线的疏密程度可以表示电场强度E的大小 | |
| C. | 电场线是直线的地方就是匀强电场 | |
| D. | 画有电场线的地方有电场,没有画电场线的地方没有电场 |
7.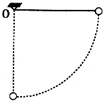 如图所示,用轻绳系一小球悬于O点.现将小球拉至水平位置,然后静止释放,不计空气阻力.小球从开始释放至摆动到最低点的过程中,下列说法正确的是( )
如图所示,用轻绳系一小球悬于O点.现将小球拉至水平位置,然后静止释放,不计空气阻力.小球从开始释放至摆动到最低点的过程中,下列说法正确的是( )
 如图所示,用轻绳系一小球悬于O点.现将小球拉至水平位置,然后静止释放,不计空气阻力.小球从开始释放至摆动到最低点的过程中,下列说法正确的是( )
如图所示,用轻绳系一小球悬于O点.现将小球拉至水平位置,然后静止释放,不计空气阻力.小球从开始释放至摆动到最低点的过程中,下列说法正确的是( )| A. | 小球的机械能守恒 | B. | 小球所受的合力不变 | ||
| C. | 小球的动能不断增大 | D. | 重力做的功等于重力势能的减少量 |
 如图所示,水平放置的两平行金属导轨间距L=0.5m,所接电源的电动势E=1.5V,内阻r=0.2Ω,金属棒的电阻R=2.8Ω,与平行导轨垂直,其余电阻不计,金属棒处于磁感应强度B=2.0T、方向与水平方向成60°角的匀强磁场中.在接通电路后金属棒还是静止,则
如图所示,水平放置的两平行金属导轨间距L=0.5m,所接电源的电动势E=1.5V,内阻r=0.2Ω,金属棒的电阻R=2.8Ω,与平行导轨垂直,其余电阻不计,金属棒处于磁感应强度B=2.0T、方向与水平方向成60°角的匀强磁场中.在接通电路后金属棒还是静止,则


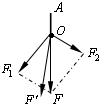
 如图所示,电子由静止开始经电压为U1的加速电场后进入AB极板组成的平行板电容器,若电子从AB极板正中间射入,电子正好能穿出电场.已知:电子的电量为e,质量为m,AB两极板间的电压为U2,距离为d,重力不计,求:
如图所示,电子由静止开始经电压为U1的加速电场后进入AB极板组成的平行板电容器,若电子从AB极板正中间射入,电子正好能穿出电场.已知:电子的电量为e,质量为m,AB两极板间的电压为U2,距离为d,重力不计,求: