题目内容
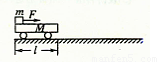
如右图所示，质量为m的物体恰好能在倾角为α的斜面上匀速下滑，如在物体上施加一个力F使物体沿斜面匀速上滑，为了使得力F取最小值，这个力与斜面的倾斜角θ为多大？这个力的最小值是多少？（设斜面长l）分析：先根据物体恰好匀速下滑求出摩擦因数，然后根据平衡条件列方程求解．
解答：解：物体从斜面的上端恰好能匀速下滑，由平衡条件得?：
mg sin α=μmg cos α
μ=tg α
在F的作用下物体向斜面上运动的过程中，F的沿斜面分量及物体与斜面间的滑动摩擦力均与θ角的大小有关，在力F拉物体沿斜面匀速上升时，根据物体的平衡条件得（选沿斜面向上方向为x轴正方向，垂直于斜面向上为y轴正方向）：?
F cosθ-mg sin α-f=0（1）
F sinθ+N-mg cos α=0（2）
其中N为斜面对物体的支持力，且f=μN=tanαN．由（1）、（2）两式可以解得?
F=
mg
上式中分子（sin α+μ cos α）mg是一个确定值，F的大小随分母变化．分母
?cosθ+μsinθ=
[
cosθ+
sinθ]=sin（φ+θ）?
当?sin（φ+θ）=1，即φ+θ=90°时，分母最大F最小．
因为φ=arctg
，所以θ=90°-φ=arctgμ时F取小值
mg．
答：以θ=arctgμ时F取小值
mg．
mg sin α=μmg cos α
μ=tg α
在F的作用下物体向斜面上运动的过程中，F的沿斜面分量及物体与斜面间的滑动摩擦力均与θ角的大小有关，在力F拉物体沿斜面匀速上升时，根据物体的平衡条件得（选沿斜面向上方向为x轴正方向，垂直于斜面向上为y轴正方向）：?
F cosθ-mg sin α-f=0（1）
F sinθ+N-mg cos α=0（2）
其中N为斜面对物体的支持力，且f=μN=tanαN．由（1）、（2）两式可以解得?
F=
| sinα+μcosα |
| cosθ+μsinθ |
上式中分子（sin α+μ cos α）mg是一个确定值，F的大小随分母变化．分母
?cosθ+μsinθ=
| 1+μ |
| 1 | ||
|
| μ | ||
|
当?sin（φ+θ）=1，即φ+θ=90°时，分母最大F最小．
因为φ=arctg
| 1 |
| μ |
| sinα+μcosα | ||
|
答：以θ=arctgμ时F取小值
| sinα+μcosα | ||
|
点评：本题考查了受力分析以及力的平衡，关键是分析数学解析式的极值问题，难度稍大．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如右图所示，质量为m的小物块以初速度v0冲上足够长的固定斜面，斜面倾角为θ，物块与该斜面间的动摩擦因数μ＜tanθ，（规定沿斜面向上方向为速度v和摩擦力f的正方向）则下图中表示该物块的速度v和所摩擦力f随时间t变化的图象正确的是（ ）
如右图所示一个质量为m物体在高为h，倾角为θ的不光滑斜面上由静止下滑，到C点静止，物体在斜面上克服摩擦力做的功为Wf，在水平面上物体所受的摩擦力为f，AC的距离为s，下列根据动能定理列出的等式正确的是（ ）
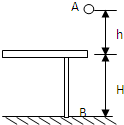如右图所示，质量为m的小球，从桌面以上h高处的A点下落到地面上的B点，桌面的高度为H，若选桌面为参考平面，设小球在A、B两点的重力势能分别为Ep1和Ep2，则（ ）
| A、Ep1=-mgh，Ep2=mgH | B、Ep1=mg（h+H），Ep2=0 | C、Ep1=mgh，Ep2=-mgH | D、Ep1=0，Ep2=-mg（h+H） |
