题目内容
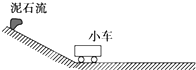
(12分)2012年10月4日,云南省彝良县发生特大泥石流,一汽车停在小山坡底,突然司机发现在距坡底240 m的山坡处泥石流以8 m/s的初速度、0.4 m/s2的加速度匀加速倾泻而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动。已知司机的反应时间为1 s,汽车启动后以0.5 m/s2的加速度一直做匀加速直线运动。试分析汽车能否安全脱离?

【答案】
司机能安全脱离
【解析】设泥石流到达坡底的时间为t1,速率为v1,则
s1=v0t1+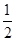 a1t12 (2分)
a1t12 (2分)
v1=v0+a1t1 (2分)
代入数值得t1=20 s,v1=16 m/s
而汽车在19 s的时间内发生位移为s2=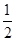 a2t22=90.25 m (2分)
a2t22=90.25 m (2分)
速度为v2=a2t2=9.5 m/s (2分)
令再经时间t3,泥石流追上汽车,则有
v1t3=s2+v2t3+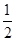 a2t32
(2分)
a2t32
(2分)
代入数值并化简得t32-26t3+361=0,因Δ<0,方程无解。所以泥石流无法追上汽车,司机能安全脱离。 (2分)
本题考查匀变速直线运动的应用,设泥石流到达坡底的时间为t1,速率为v1,由位移和时间的关系式、速度与加速度的关系式可求得运动时间和末速度,汽车在19s发生的位移根据运动学公式可求得,与泥石流的位移进行对比可知泥石流无法追上汽车

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 2012年10月4日,云南省彝良县发生特大泥石流,一汽车停在小山坡底,突然司机发现在距坡底240m的山坡处泥石流以8m/s的初速度、0.4 m/s2的加速度匀加速倾泻而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动.已知司机的反应时间为1s,汽车启动后以0.5m/s2的加速度一直做匀加速直线运动.试通过计算说明汽车能否安全脱离?
2012年10月4日,云南省彝良县发生特大泥石流,一汽车停在小山坡底,突然司机发现在距坡底240m的山坡处泥石流以8m/s的初速度、0.4 m/s2的加速度匀加速倾泻而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动.已知司机的反应时间为1s,汽车启动后以0.5m/s2的加速度一直做匀加速直线运动.试通过计算说明汽车能否安全脱离?