题目内容
18. 长方形木板质量为M,在光滑的水平面上做匀速运动,速度为V0,此时将质量为m的物体轻轻放在P点,物体与木板间的动摩擦因数为μ,求:
长方形木板质量为M,在光滑的水平面上做匀速运动,速度为V0,此时将质量为m的物体轻轻放在P点,物体与木板间的动摩擦因数为μ,求:(1)物体与木板相对静止时,木板的速度?
(2)与木板相对静止时,物体与P点的距离?
分析 (1)根据牛顿第二定律分别求出木板和物块的加速度,结合速度相等求出运动的时间,从而结合速度时间公式求出木板的速度.
(2)根据速度位移公式分别求出木块和木板的位移,从而得出与木板相对静止时,物体与P点的距离.
解答 解:(1)物体放上木板后,物块的加速度a1=μg,
木板的加速度${a}_{2}=\frac{μmg}{M}$,
当两者速度相等时,有:a1t=v0-a2t,
解得$t=\frac{{v}_{0}}{{a}_{1}+{a}_{2}}$,
此时木板的速度v=a1t,
联立解得v=$\frac{M{v}_{0}}{M+m}$.
(2)物体与P点的距离为:
$△x=\frac{{{v}_{0}}^{2}-{v}^{2}}{2{a}_{2}}-\frac{{v}^{2}}{2{a}_{1}}$=$\frac{M{{v}_{0}}^{2}}{2μ(M+m)g}$.
答:(1)物体与木板相对静止时,木板的速度为$\frac{M{v}_{0}}{M+m}$.
(2)与木板相对静止时,物体与P点的距离为$\frac{M{{v}_{0}}^{2}}{2μ(M+m)g}$.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,抓住速度相等,结合运动学公式和牛顿第二定律进行求解,本题也可以 根据动量守恒定律和能量守恒定律进行求解.

练习册系列答案
相关题目
8.有关交流电的下列说法不正确的是( )
| A. | 交变电流的有效值实质就是平均值 | |
| B. | 只有正(或余)弦式电流才有U=$\frac{{U}_{m}}{\sqrt{2}}$的关系 | |
| C. | 照明电压220V、动力电压380V,交流电压表和电流表测量的值指的都是交变电流的有效值 | |
| D. | 交变电流u=311sin314t的相位是314t,初相是0 |
6.以下关于热力学知识的叙述正确的是( )
| A. | 绝热过程是指系统不从外界吸热,也不向外界放热,这个过程不与外界交换能量 | |
| B. | 热量是在单纯的热传递过程中系统内能变化的量度,所以不能说物体具有多少热量,只能说物体吸收或放出多少热量 | |
| C. | 悬浮在液体中的微粒越小,在某一瞬间跟它相撞的液体分子数越少,撞击作用的不平衡性就表现得越明显,因而布朗运动越明显 | |
| D. | 由熵的定义可知,熵较大的宏观状态就是无序程度很小的宏观状态,也就是出现概率较小的宏观状态 |
13.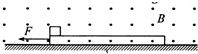 如图所示,空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速放置一质量为0.1㎏、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.现对木板施加方向水平向左,大小为0.6N的恒力,g取10m/s2.则( )
如图所示,空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速放置一质量为0.1㎏、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.现对木板施加方向水平向左,大小为0.6N的恒力,g取10m/s2.则( )
 如图所示,空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速放置一质量为0.1㎏、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.现对木板施加方向水平向左,大小为0.6N的恒力,g取10m/s2.则( )
如图所示,空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速放置一质量为0.1㎏、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.现对木板施加方向水平向左,大小为0.6N的恒力,g取10m/s2.则( )| A. | 木板和滑块一直做加速度为2m/s2的匀加速运动 | |
| B. | 滑块开始做匀加速运动,然后做匀速直线运动 | |
| C. | 最终木板做加速度为2m/s2的匀加速运动,滑块做速度为10m/s的匀速运动 | |
| D. | 最终木板做加速度为3m/s2的匀加速运动,滑块做速度为10m/s的匀速运动 |
3.在水平面上有一个小物块质量为m,从某点给它一个初速度沿水平面做匀减速直线运动,先后经过A、B、C三点到O点速度为零.A、B、C三点到O点距离分别为x1、x2、x3,时间分别为t1、t2、t3,下列结论正确的是( )
| A. | $\frac{{x}_{1}}{{t}_{1}}$=$\frac{{x}_{2}}{{t}_{2}}$=$\frac{{x}_{3}}{{t}_{3}}$ | B. | $\frac{{x}_{1}}{{t}_{1}}$<$\frac{{x}_{2}}{{t}_{2}}$<$\frac{{x}_{3}}{{t}_{3}}$ | ||
| C. | $\frac{{x}_{1}}{{{t}_{1}}^{2}}$=$\frac{{x}_{2}}{{{t}_{2}}^{1}}$=$\frac{{x}_{3}}{{t}_{{3}^{2}}}$ | D. | $\frac{{x}_{1}}{{{t}_{1}}^{2}}$<$\frac{{x}_{2}}{{{t}_{2}}^{1}}$<$\frac{{x}_{3}}{{t}_{{3}^{2}}}$ |
7.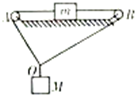 物体M、m分别用跨过光滑定滑轮的轻绳相连如图放置,OA、OB与水平面的夹角分别为53°和37°,物体M、m的重力分别为20N和10N,m与水平面的动摩擦因数为0.5,M、m的初速度都为零,则( )
物体M、m分别用跨过光滑定滑轮的轻绳相连如图放置,OA、OB与水平面的夹角分别为53°和37°,物体M、m的重力分别为20N和10N,m与水平面的动摩擦因数为0.5,M、m的初速度都为零,则( )
 物体M、m分别用跨过光滑定滑轮的轻绳相连如图放置,OA、OB与水平面的夹角分别为53°和37°,物体M、m的重力分别为20N和10N,m与水平面的动摩擦因数为0.5,M、m的初速度都为零,则( )
物体M、m分别用跨过光滑定滑轮的轻绳相连如图放置,OA、OB与水平面的夹角分别为53°和37°,物体M、m的重力分别为20N和10N,m与水平面的动摩擦因数为0.5,M、m的初速度都为零,则( )| A. | 绳OA对M的拉力大小为12N | |
| B. | 绳OB对M的拉力大小为16N | |
| C. | m受到水平面的摩擦力大小为10N,方向水平向左 | |
| D. | m受到水平面的摩擦力大小为4N,方向水平向右 |