题目内容
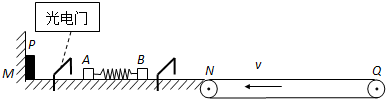
研究物体的运动时,常常用到光电计时器.如图所示,当有不透光的物体通过光电门时,光电计时器就可以显示出物体的挡光时间.光滑水平导轨MN上放置两个物块A和B,左端挡板处有一弹射装置P,右端N处与水平传送带平滑连接,将两个宽度为d=3.6×10-3m的遮光条分别安装在物块A和B上,且高出物块,并使遮光条在通过光电门时挡光.传送带水平部分的长度L=9.0m,沿逆时针方向以恒定速度v=6.0m/s匀速转动.物块B与传送带的动摩擦因数μ=0.20,物块A的质量(包括遮光条)为mA=2.0kg.开始时在A和B之间压缩一轻弹簧,锁定其处于静止状态,现解除锁定,弹开物块A和B,迅速移去轻弹簧.两物块第一次通过光电门,物块A通过计时器显示的读数t1=9.0×10-4s,物块B通过计时器显示的读数t2=1.8×10-3s,重力加速度g取10m/s2,试求:
(1)弹簧储存的弹性势能Ep;
(2)物块B在传送带上滑行的过程中产生的内能;
(3)若物体B返回水平面MN后与被弹射装置P弹回的A在水平面上相碰,碰撞中没有机械能损失,则弹射装置P必须对A做多少功才能让B碰后从Q端滑出.
(1)弹簧储存的弹性势能Ep;
(2)物块B在传送带上滑行的过程中产生的内能;
(3)若物体B返回水平面MN后与被弹射装置P弹回的A在水平面上相碰,碰撞中没有机械能损失,则弹射装置P必须对A做多少功才能让B碰后从Q端滑出.

分析:(1)解除锁定弹簧弹开物块AB后,两块都做匀速运动,根据通过光电门的时间和d,求出两物块的速度,根据动量守恒定律和机械能守恒定律求出弹簧储存的弹性势能Ep;
(2)B滑上传送带后先向右做匀减速运动,当速度减小为零时,向右滑行的距离最远.根据牛顿第二定律求出B的加速度,由速度位移公式求出向右运动的最大位移和时间,求出此时间内传送带运动的距离,得到两者相对位移大小.当物块B返回时,再求出两者相对位移大小,即可由Q=μmBg△x求解内能.
(3)根据功能关系得到弹射装置对A做功W与弹射前后A的速度关系.AB碰撞中动量和机械能都守恒,列出两个守恒方程.B要刚好能滑出平台Q端,碰后B的动能大于克服摩擦力做功,联立求解弹射装置P必须对A做多少功.
(2)B滑上传送带后先向右做匀减速运动,当速度减小为零时,向右滑行的距离最远.根据牛顿第二定律求出B的加速度,由速度位移公式求出向右运动的最大位移和时间,求出此时间内传送带运动的距离,得到两者相对位移大小.当物块B返回时,再求出两者相对位移大小,即可由Q=μmBg△x求解内能.
(3)根据功能关系得到弹射装置对A做功W与弹射前后A的速度关系.AB碰撞中动量和机械能都守恒,列出两个守恒方程.B要刚好能滑出平台Q端,碰后B的动能大于克服摩擦力做功,联立求解弹射装置P必须对A做多少功.
解答:解:(1)解除锁定弹开AB后,AB两物体的速度大小:
又vA=
=
m/s=4m/s
vB=
=
m/s=2m/s
根据系统的动量守恒得:mAvA=mBvB;
解得:mB=
=
kg=4kg
所以弹簧储存的弹性势能 EP=
mA
+
mB
=24J
(2)B滑上传送带匀减速运动,当速度减为零时,滑动的距离最远.
由牛顿第二定律得:μmBg=mBa,得a=2m/s2.
B向右运动的距离为 x1=
=1m<L,则物块将返回,向右运动的时间为
t1=
=1s
传送带向左运动的距离为x2=vt1=6m
则B相对于传送带的位移为△x1=x1+x2=7m
设B向左返回所用时间仍为t1,位移为x1,B相对于传送带的位移为△x2=x2-x1=5m
故物块B在传送带上滑行的过程中产生的内能为
Q=μmBg(△x1+△x2)=96J
(3)设弹射装置对A做功为W,则:
mA
=
mA
+W ①
AB相碰,碰前B的速度为vB=2m/s,设碰后B的速度为vB′,则
根据动量守恒和机械能守恒得
mAvA′-mBvB=mAvA″+mBvB′②
mA
+
mB
=
mA
+
mB
③
B要刚好能滑出平台Q端,由能量关系有:
mB
>μmBgL ④
代入解④得:vB′>6m/s
代入解②③得:vA′=1.5vB′+0.5vB>(1.5×6+1)m/s=10m/s
由①得:W>84J
答:
(1)弹簧储存的弹性势能Ep是24J.
(2)物块B在传送带上滑行的过程中产生的内能是96J;
(3)弹射装置P必须对A做84J功才能让B碰后从Q端滑出.
又vA=
| d |
| t1 |
| 3.6×10-3 |
| 9×10-4 |
vB=
| d |
| t2 |
| 3.6×10-3 |
| 1.8×10-3 |
根据系统的动量守恒得:mAvA=mBvB;
解得:mB=
| mAvA |
| vB |
| 2×4 |
| 2 |
所以弹簧储存的弹性势能 EP=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
(2)B滑上传送带匀减速运动,当速度减为零时,滑动的距离最远.
由牛顿第二定律得:μmBg=mBa,得a=2m/s2.
B向右运动的距离为 x1=
| ||
| 2a |
t1=
| vB |
| a |
传送带向左运动的距离为x2=vt1=6m
则B相对于传送带的位移为△x1=x1+x2=7m
设B向左返回所用时间仍为t1,位移为x1,B相对于传送带的位移为△x2=x2-x1=5m
故物块B在传送带上滑行的过程中产生的内能为
Q=μmBg(△x1+△x2)=96J
(3)设弹射装置对A做功为W,则:
| 1 |
| 2 |
| v | ′2 A |
| 1 |
| 2 |
| v | 2 A |
AB相碰,碰前B的速度为vB=2m/s,设碰后B的速度为vB′,则
根据动量守恒和机械能守恒得
mAvA′-mBvB=mAvA″+mBvB′②
| 1 |
| 2 |
| v | ′2 A |
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | ″2 A |
| 1 |
| 2 |
| v | ′2 B |
B要刚好能滑出平台Q端,由能量关系有:
| 1 |
| 2 |
| v | ′2 B |
代入解④得:vB′>6m/s
代入解②③得:vA′=1.5vB′+0.5vB>(1.5×6+1)m/s=10m/s
由①得:W>84J
答:
(1)弹簧储存的弹性势能Ep是24J.
(2)物块B在传送带上滑行的过程中产生的内能是96J;
(3)弹射装置P必须对A做84J功才能让B碰后从Q端滑出.
点评:本题是复杂的力学综合题,综合了运动学公式、牛顿第二定律、机械能守恒、动量守恒等多个知识,分析运动过程,选择解题规律是关键.

练习册系列答案
相关题目
关于参考系的选取,下列说法中正确的是( )
| A、研究物体的运动,必须选定参考系 | B、描述一个物体的运动情况时,参考系是可以任意选取的 | C、实际选取参考系时,应本着便于观测和使对运动的描述尽可能简单的原则来进行,如研究地面上的运动时,常取地面或相对于地面静止的其他物体做参考系 | D、参考系必须选取地面或相对于地面不动的其他物体 |