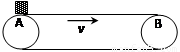题目内容
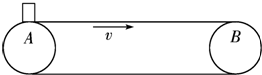如图所示为一平直传送带，A、B两处间的距离为L，传送带的运动速度恒为v．有一工件轻轻从A处放上传送带，已知工件与传送带间的动摩擦因数为μ，及当地的重力加速度为g，且认为传送带的形状及速率不受影响．求传送带将该工件由A处送到B处可能的时间间隔△t及相应的条件．（即题中给出量之间应满足的关系）．
解：工件放上传送带受到水平向右的摩擦力f=μmg
由牛顿第二定律，可得a=
=μg
则工件加速时间为t=
=
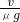
此过程工件运动的位移s=
at2=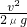
①若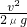≥L，则工件一直加速到B点，
可得L=at2，得△t=
②若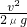＜L，则工件先加速至v后做匀速运动直到B
△t=t+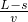
=
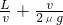
答：若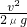≥L，△t=；若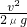＜L，△t=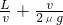
分析：先求出工件的加速度，再求出工件匀加速速度达到v时的位移，根据此位移与L的关系进行讨论即可求解．
点评：本题主要考查了牛顿第二定律及运动学基本公式的应用，要分两种情况进行讨论，难度适中．
由牛顿第二定律，可得a=
=μg 则工件加速时间为t=
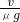
=此过程工件运动的位移s=
at2=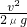①若
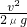≥L，则工件一直加速到B点，可得L=
at2，得△t=②若
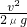＜L，则工件先加速至v后做匀速运动直到B△t=t+
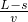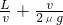
= 答：若
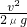≥L，△t=；若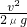＜L，△t=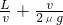分析：先求出工件的加速度，再求出工件匀加速速度达到v时的位移，根据此位移与L的关系进行讨论即可求解．
点评：本题主要考查了牛顿第二定律及运动学基本公式的应用，要分两种情况进行讨论，难度适中．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
如图所示，一平直的传送带以速度v=2m/s匀速运动，传送带把A处的工件运送到B处，A、B相距L=10m．从A处把工件无初速地放到传送带上，经过时间t=6s能传送到B处．求：
