题目内容
甲车停在平直公路上,乙车以速度v0=20m/s从甲车旁驶过,同时甲车启动开始追赶乙车。已知甲车的启动加速度为a=5m/s2,达到其最大速度v=30m/s后做匀速运动。试问:
(1)甲车追上乙车时是在加速阶段还是匀速阶段?
(2)甲车追上乙车一共所花的时间是多少?
(1)甲车追上乙车必然在匀速阶段(2)t=9s
【解析】(1)经时间t0甲车达到最大速度,有
v=at0
带入数据得t0=6s (1)
甲车位移
x1=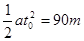 (2)
(2)
乙车位移
x2=v0t0=120m (3)
因为x1< x2,所以甲车追上乙车必然在匀速阶段
(2)设甲车追上乙车共花时间t
甲车位移为
s1=x1+v(t-t0) (4)
乙车位移为
s2=v0t (5)
甲车追上乙车时
s1=s2 (6)
由(4)(5)(6)解得
t=9s (7)
评分标准:
(1)问4分,只要判断方法正确都给分,没有判断依据不给分。
(2)问6分,(4)(5)各2分,(6)(7)各1分。
本题考查匀变速直线运动中的追击相遇问题,判断在哪个阶段追上乙车,可用假设法判断,假设匀加速阶段追上,由v=at可计算出速度增大到最大时所用的时间,由此求得乙车位移大小,再由位移与时间的关系求得甲车速度增大到最大时的位移,两个位移比较大小就能判断,在匀速阶段追上乙车,先计算出匀加速阶段位移和时间,设加速t时刻后追上乙车,由时间和位移上的等量关系列公式求解

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案