题目内容
 (A)我国2010年10月1号成功发射了探月卫星“嫦娥二号”.嫦娥二号卫星绕月工作轨道可近似看作圆轨道,已知其轨道高度为h,运行周期为T,月球平均半径为R,则嫦娥二号卫星绕月运行的加速度大小为
(A)我国2010年10月1号成功发射了探月卫星“嫦娥二号”.嫦娥二号卫星绕月工作轨道可近似看作圆轨道,已知其轨道高度为h,运行周期为T,月球平均半径为R,则嫦娥二号卫星绕月运行的加速度大小为| 4π2(R+h) |
| T2 |
| 4π2(R+h) |
| T2 |
| 4π2(R+h)3 |
| T2R2 |
| 4π2(R+h)3 |
| T2R2 |
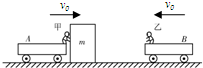
(B)如图所示,甲、乙两个小孩分别站在A、B两辆冰车上,甲与A车的总质量为30kg,乙和B车的总质量也为30kg.甲推着一个质量为15kg的箱子和他一起以大小为v0=2.0m/s的速度滑行,乙以同样大小的速度迎面滑来,甲突然将箱子沿冰面推给乙,箱子滑动到乙处时,乙迅速把它抓住,若不计冰面的摩擦力,为了避免与乙相撞,甲推箱子的速度大小(相对地面)至少为
5.2
5.2
m/s,甲推箱子时对箱子做功为172.8
172.8
J.分析:(A)嫦娥二号卫星绕月做匀速圆周运动,轨道半径为R+h,月球对卫星万有引力提供卫星的向心力,根据圆周运动的公式和牛顿第二定律求解卫星绕月运行的加速度大小和月球表面的重力加速度大小.
(B)甲将箱子沿冰面推给乙过程,甲乙的总动量守恒,乙把箱子抓住过程,乙与箱子总电量守恒,当甲与乙恰好不相撞时,甲将箱子推给乙后速度与乙接住箱子后的速度恰好相等.根据动量守恒定律和速度相等条件求解甲推箱子的速度大小的最小值.根据动能定理求出甲推箱子时对箱子做功.
(B)甲将箱子沿冰面推给乙过程,甲乙的总动量守恒,乙把箱子抓住过程,乙与箱子总电量守恒,当甲与乙恰好不相撞时,甲将箱子推给乙后速度与乙接住箱子后的速度恰好相等.根据动量守恒定律和速度相等条件求解甲推箱子的速度大小的最小值.根据动能定理求出甲推箱子时对箱子做功.
解答:解:(A)卫星绕月运行的加速度大小a=
设卫星的质量为m,月球的质量为M,根据牛顿第二定律得
G
=m
①
设在月球表面上,某物体质量为m′,月球表面的重力加速度大小为g
则m′g=G
②
联立①②得
g=
(B)根据动量守恒得
(m甲+m)v0=m甲v甲+mv,①
mv-mv乙=(m+m乙)v乙,②
当甲与乙恰好不相撞时,v甲=v乙,③
联立①②③得v=5.2m/s
甲推箱子时对箱子做功W=
mv2-
m
=172.8J
故本题答案是:(A)
;
(B)5.2;172.8
| 4π2(R+h) |
| T2 |
设卫星的质量为m,月球的质量为M,根据牛顿第二定律得
G
| Mm |
| (R+h)2 |
| 4π2(R+h) |
| T2 |
设在月球表面上,某物体质量为m′,月球表面的重力加速度大小为g
则m′g=G
| Mm′ |
| R2 |
联立①②得
g=
| 4π2(R+h)3 |
| T2R2 |
(B)根据动量守恒得
(m甲+m)v0=m甲v甲+mv,①
mv-mv乙=(m+m乙)v乙,②
当甲与乙恰好不相撞时,v甲=v乙,③
联立①②③得v=5.2m/s
甲推箱子时对箱子做功W=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
故本题答案是:(A)
| 4π2(R+h) |
| T2 |
| 4π2(R+h)3 |
| T2R2 |
(B)5.2;172.8
点评:对于卫星问题基本思路是:卫星做匀速圆周运动,万有引力提供向心力.对于第(B)题,关键在于分析过程,选择规律,难点是不相撞的条件.

练习册系列答案
相关题目
 :1
:1