题目内容
12.在电梯地板上摆放一台秤,台秤上有一物体,如果读数与物体重力有下列偏差,则下列判断正确的是( )| A. | 读数偏大,则电梯一定是在向上做加速运动 | |
| B. | 读数偏小,则电梯一定是在向下做减速运动 | |
| C. | 读数偏大,则电梯可能是在向下做减速运动 | |
| D. | 读数准确,则电梯可能静止,也可能在运动 |
分析 对物体受力分析,然后根据牛顿第二定律求解加速度,再确定物体的运动情况,然后结合超重与失重解答即可.
解答 解:AC、当电梯运动时,看到弹簧秤的度数为偏大,物体受向上的弹力,向下的重力,根据牛顿第二定律,有:
F-G=ma
由于F大于G,故加速度向上,处于超重状态,故电梯加速上升或者减速下降;故A错误;C正确;
B、看到弹簧秤的度数为偏小,由于F小于G,故加速度向下,处于失重状态,故电梯加速下降或者减速上升.故B错误;
D、读数准确,则装置处于平衡状态,有可能静止,也可能是向上或向下做匀速运动.故D正确.
故选:CD
点评 本题关键对物体受力分析后根据牛顿第二定律确定加速度,然后得到运动情况,明确加速度向上有可能为加速向下,也有可有减速向下.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
2.自世界上第一颗人造卫星以来,人类的活动范围逐步扩展,现在已成功地把人造天体送到火星上漫步,我国也已实现载人航天飞行,并着手实施登月计划.下列有关人造天体的说法中正确的是( )
| A. | 卫星的轨道越高,其运转速度越大,周期越大 | |
| B. | 若地球没有自转,地球将没有同步卫星 | |
| C. | 卫星的质量一定时,轨道半径越大,它需要的向心力越大 | |
| D. | 做匀速圆周运动的载人空间站中,宇航员仍受重力的作用,但所受合外力为零 |
3. 2008年9月27日“神舟七号”宇航员翟志刚顺利完成出舱活动任务,他的第一次太空街标志着中国航天事业全新时代的到来,“神舟七号”绕地球近似做匀速圆周运动,其轨道半径为r,若另有一颗卫星绕地球做匀速圆周运动的半径为3r,则可以确定( )
2008年9月27日“神舟七号”宇航员翟志刚顺利完成出舱活动任务,他的第一次太空街标志着中国航天事业全新时代的到来,“神舟七号”绕地球近似做匀速圆周运动,其轨道半径为r,若另有一颗卫星绕地球做匀速圆周运动的半径为3r,则可以确定( )
 2008年9月27日“神舟七号”宇航员翟志刚顺利完成出舱活动任务,他的第一次太空街标志着中国航天事业全新时代的到来,“神舟七号”绕地球近似做匀速圆周运动,其轨道半径为r,若另有一颗卫星绕地球做匀速圆周运动的半径为3r,则可以确定( )
2008年9月27日“神舟七号”宇航员翟志刚顺利完成出舱活动任务,他的第一次太空街标志着中国航天事业全新时代的到来,“神舟七号”绕地球近似做匀速圆周运动,其轨道半径为r,若另有一颗卫星绕地球做匀速圆周运动的半径为3r,则可以确定( )| A. | 卫星与“神舟七号”的向心力大小之比为1:9 | |
| B. | 卫星与“神舟七号”的线速度大小之比为1:$\sqrt{3}$ | |
| C. | 卫星与“神舟七号”的动能之比为1:3 | |
| D. | 卫星与“神舟七号”的周期之比为3$\sqrt{3}$:1 |
20.一质量为m的物体静止在粗糙水平地面上,现用一大小为F的水平拉力拉动物体,经过一段时间后其速度变为v,重力加速度为g,则( )
| A. | 在这段时间内,摩擦力做的功为零 | |
| B. | 在这段时间内,拉里做的功为$\frac{1}{2}$mv2 | |
| C. | 物体的速度为v时,拉力的功率为Fv | |
| D. | 物体的速度为v时,重力的功率为mgv |
7. 如图所示,为一环境温度监控电器,R1为灯泡,R2为半导体材料制成的热敏电阻(电阻随温度升高而变小),当环境温度降低时则有( )
如图所示,为一环境温度监控电器,R1为灯泡,R2为半导体材料制成的热敏电阻(电阻随温度升高而变小),当环境温度降低时则有( )
 如图所示,为一环境温度监控电器,R1为灯泡,R2为半导体材料制成的热敏电阻(电阻随温度升高而变小),当环境温度降低时则有( )
如图所示,为一环境温度监控电器,R1为灯泡,R2为半导体材料制成的热敏电阻(电阻随温度升高而变小),当环境温度降低时则有( )| A. | 灯泡的亮度变亮,电路中消耗的总功率P变小 | |
| B. | 灯泡的亮度变亮,电路中消耗的总功率P变大 | |
| C. | 灯泡的亮度变暗,电路中消耗的总功率P变小 | |
| D. | 灯泡的亮度变暗,电路中消耗的总功率P变大 |
1. 如图所示,小球自a点由静止自由下落,到b点时与竖直弹簧接触,d点是小球运动的最低点,bc=cd.不计弹簧质量和空气阻力,小球在由a到d向下运动过程中,下列说法正确的是( )
如图所示,小球自a点由静止自由下落,到b点时与竖直弹簧接触,d点是小球运动的最低点,bc=cd.不计弹簧质量和空气阻力,小球在由a到d向下运动过程中,下列说法正确的是( )
 如图所示,小球自a点由静止自由下落,到b点时与竖直弹簧接触,d点是小球运动的最低点,bc=cd.不计弹簧质量和空气阻力,小球在由a到d向下运动过程中,下列说法正确的是( )
如图所示,小球自a点由静止自由下落,到b点时与竖直弹簧接触,d点是小球运动的最低点,bc=cd.不计弹簧质量和空气阻力,小球在由a到d向下运动过程中,下列说法正确的是( )| A. | 小球的机械能守恒 | |
| B. | 小球在b点时其重力做功功率最大 | |
| C. | 到c点时小球的动能最大 | |
| D. | 由a到d的整个过程中小球重力势能的减小量等于弹簧弹性势能的增加量 |
18.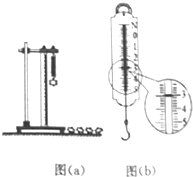 某同学利用如图(a)所示的装置做“探究弹簧测力计大小与其长度的关系”的实验.
某同学利用如图(a)所示的装置做“探究弹簧测力计大小与其长度的关系”的实验.
(1)在安装刻度尺时,必须使刻度尺保持竖直状态.
(2)下表是他实验测得的该弹簧测力计大小F与弹簧长度x的关系的几组数据:
由表中数据可得,该弹簧的原长x0=4.0cm,劲度系数k=50N/m.
(3)他又利用实验原理把该弹簧做成一把弹簧秤,当弹簧秤上的示数如图(b)示数时,该弹簧的长度x=10.0cm.
 某同学利用如图(a)所示的装置做“探究弹簧测力计大小与其长度的关系”的实验.
某同学利用如图(a)所示的装置做“探究弹簧测力计大小与其长度的关系”的实验.(1)在安装刻度尺时,必须使刻度尺保持竖直状态.
(2)下表是他实验测得的该弹簧测力计大小F与弹簧长度x的关系的几组数据:
| 弹簧弹力F/N | 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 弹簧的长度x/cm | 4.0 | 6.0 | 8.0 | 10.0 | 12.0 | 14.0 | 16.0 |
(3)他又利用实验原理把该弹簧做成一把弹簧秤,当弹簧秤上的示数如图(b)示数时,该弹簧的长度x=10.0cm.
19. 如图所示,长为L的轻杆一端固定重力为m的小球(可视为质点),另一端有固定转轴O.现使小球在竖直平面内做圆周运动,P为圆周轨道的最高点.若小球通过圆周轨道最低点时的速度大小为$\sqrt{\frac{9}{2}gL}$,则小球( )
如图所示,长为L的轻杆一端固定重力为m的小球(可视为质点),另一端有固定转轴O.现使小球在竖直平面内做圆周运动,P为圆周轨道的最高点.若小球通过圆周轨道最低点时的速度大小为$\sqrt{\frac{9}{2}gL}$,则小球( )
 如图所示,长为L的轻杆一端固定重力为m的小球(可视为质点),另一端有固定转轴O.现使小球在竖直平面内做圆周运动,P为圆周轨道的最高点.若小球通过圆周轨道最低点时的速度大小为$\sqrt{\frac{9}{2}gL}$,则小球( )
如图所示,长为L的轻杆一端固定重力为m的小球(可视为质点),另一端有固定转轴O.现使小球在竖直平面内做圆周运动,P为圆周轨道的最高点.若小球通过圆周轨道最低点时的速度大小为$\sqrt{\frac{9}{2}gL}$,则小球( )| A. | 不能到达P点 | |
| B. | 到达P点时的速度大于$\sqrt{gL}$ | |
| C. | 能到达P,但在P点不会受到轻杆的弹力 | |
| D. | 能达到P点,且在P点受到轻杆向上的支持力 |
 如图在一矩形区域内,不加磁场时,不计重力的带电粒子以某一初速度垂直左边界射入,穿过区域的时间为t0,若加上磁感应强度为B,水平向里的匀强磁场,带电粒子仍以原来的初速度入射,粒子飞出偏离原方向30°.求:
如图在一矩形区域内,不加磁场时,不计重力的带电粒子以某一初速度垂直左边界射入,穿过区域的时间为t0,若加上磁感应强度为B,水平向里的匀强磁场,带电粒子仍以原来的初速度入射,粒子飞出偏离原方向30°.求: