题目内容
19.对于绕地球表面环绕的人造地球卫星A,其向心加速度为aA、线速度为vA、角速度为wA、周期为TA;而对地球同步卫星B,其向心加速度为aB、线速度为vB、角速度为wB、周期为TB.已知地球表面重力加速度为g,第一宇宙速度为v.则下列有关说法正确的是( )| A. | TA>TB | B. | vA=v<vB | C. | aA=g>aB | D. | wA<wB |
分析 根据万有引力提供向心力得出线速度、角速度、周期与轨道半径的关系,从而得出线速度、角速度、周期之比
解答 解:万有引力提供向心力:$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}mr\frac{4{π}^{2}}{{T}^{2}}=ma$=mrω2 ①
A、由①得:$T=2π\sqrt{\frac{{r}^{3}}{GM}}$ 可知r大的T小,则TA<TB,则A错误
B、由①得$v=\sqrt{\frac{GM}{r}}$ 可知r小的v大,则vA=v>vB,则B错误
C、由①得$a=\frac{GM}{{r}^{2}}$可知aA=g>aB,则C正确
D、由①得$ω=\sqrt{\frac{GM}{{r}^{3}}}$,可知ωA>ωB,则D错误
故选:C
点评 解决本题的关键掌握万有引力提供向心力这一理论,并能灵活运用

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
9.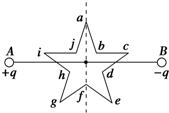 如图所示,在真空中的A、B两点分别放置等量异种点电荷,在A、B两点间取一正五角星形路径abcdefghija,五角星的中心与A、B的中点重合,其中af连线与AB连线垂直.现将一电子沿该路径逆时针移动一周,下列判断正确的是( )
如图所示,在真空中的A、B两点分别放置等量异种点电荷,在A、B两点间取一正五角星形路径abcdefghija,五角星的中心与A、B的中点重合,其中af连线与AB连线垂直.现将一电子沿该路径逆时针移动一周,下列判断正确的是( )
 如图所示,在真空中的A、B两点分别放置等量异种点电荷,在A、B两点间取一正五角星形路径abcdefghija,五角星的中心与A、B的中点重合,其中af连线与AB连线垂直.现将一电子沿该路径逆时针移动一周,下列判断正确的是( )
如图所示,在真空中的A、B两点分别放置等量异种点电荷,在A、B两点间取一正五角星形路径abcdefghija,五角星的中心与A、B的中点重合,其中af连线与AB连线垂直.现将一电子沿该路径逆时针移动一周,下列判断正确的是( )| A. | e点和g点的电场强度相同 | |
| B. | a点和f点的电势不相等 | |
| C. | 电子从g点到f点再到e点过程中,电势能一直在增大 | |
| D. | 电子从f点到e点再到d点过程中,电场力先做正功后做负功 |
7.下列说法正确的是( )
| A. | 牛顿发现了行星的运动定律 | |
| B. | 开普勒发现了万有引力定律 | |
| C. | 卡文迪许用纽秤实验测出了万有引力常量 | |
| D. | 伽利略发现了海王星和冥王星 |
4.关于描述圆周运动的物理量,下列说法正确的是( )
| A. | 质点的角速度越大说明质点运动的越快 | |
| B. | 质点的向心加速度越大说明质点线速度方向变化的越快 | |
| C. | 做圆周运动的质点的加速度方向一定指向圆心 | |
| D. | 做圆周运动的质点受到的合外力一定指向圆心 |
11.理论和实践证明,开普勒定律不仅适用于太阳系中的天体运动,而且对一切天体(包括卫星绕行星的运动)都适用.下面对于开普勒第三定律的公式$\frac{{R}^{3}}{{T}^{2}}$=K,下列说法正确的是( )
| A. | 公式只适用于轨道是椭圆的运动 | |
| B. | 式中的K值,对太阳-行星系统和地球-月球系统是相等的 | |
| C. | 式中的K值,只与中心天体有关,与绕中心天体旋转的行星(或卫星)无关 | |
| D. | 若已知月球与地球之间的距离,根据公式可求出地球与太阳之间的距离 |
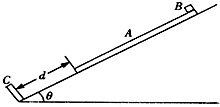 如图所示,光滑斜面倾角为θ,底端固定一垂直于斜面的挡板C.在斜面上放置长木板A,A的下端与C的距离为d,A的上端放置小物块B,A、B的质量均为m,A.B间的动摩擦因数μ>tanθ.现同时由静止释放A、B,A与C发生碰撞的时间极短,碰撞前后瞬间速度大小相等,运动过程中小物块始终没有从木板上滑落,已知重力加速度为g求:
如图所示,光滑斜面倾角为θ,底端固定一垂直于斜面的挡板C.在斜面上放置长木板A,A的下端与C的距离为d,A的上端放置小物块B,A、B的质量均为m,A.B间的动摩擦因数μ>tanθ.现同时由静止释放A、B,A与C发生碰撞的时间极短,碰撞前后瞬间速度大小相等,运动过程中小物块始终没有从木板上滑落,已知重力加速度为g求: