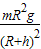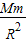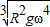题目内容
设地球同步卫星的质量为m,它距离地面的高度为h,地球的质量为M、半径为R、自转角速度为ω,地球表面的重力加速度为g,万有引力常量为G,则该同步卫星所受向心力可表示为( )
分析:由题地球的同步卫星的轨道半径为R=R0+h.其角速度等于地球自转角速度,根据地球的半径和地球表面的重力加速度,由重力等于万有引力,可求出地球的质量.由向心力公式求解向心力.或由万有引力等于向心力求解.
解答:解:A、地球同步卫星的角速度等于地球自转角速度ω,轨道半径为R=R0+h.则同步卫星所受向心力为F=mω2(R+h).故A正确.
B、C根据万有引力等于向心力,得同步卫星所受向心力为 F=
在地球表面上,有m′g=G
联立得:F=
.故B正确.C错误.
D、由F=mω2(R+h)=
,得R+h=
则得F=mω2(R+h)=mω2?
=m
.故D正确.
故选ABD
B、C根据万有引力等于向心力,得同步卫星所受向心力为 F=
| GMm |
| (R+h)2 |
在地球表面上,有m′g=G
| Mm′ |
| R2 |
联立得:F=
| mR2g |
| (R+h)2 |
D、由F=mω2(R+h)=
| mR2g |
| (R+h)2 |
| 3 |
| ||
则得F=mω2(R+h)=mω2?
| 3 |
| ||
| 3 | R2gω4 |
故选ABD
点评:此题为天体运动的典型题型,由万有引力提供向心力,再根据向心力的基本公式求解,解题过程中注意黄金代换式g=G
.
| M |
| R2 |

练习册系列答案
相关题目