题目内容
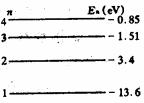
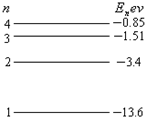
(1)如图给出氢原子最低的4个能级,一群氢原子处于量子数最高为4的能级,这些氢原子跃迁所辐射的光子的频率最多有________种,其中最小频率为________,要使基态氢原子电离,应用波长为________的光照射氢原子(已知h=6.63×10-34 J·s).

(2)光滑水平地面上停放着甲、乙两辆平板车,一根轻绳跨过乙车的定滑轮(不计定滑轮的质量和摩擦),绳的一端与甲车相连,另一端被甲车上的人拉在手中,已知每辆车和人的质量均为30 kg,两车间的距离足够远.现在人用力拉绳,两车开始相向运动,人与甲车保持相对静止,当乙车的速度为0.5 m/s时,停止拉绳.

①人在拉绳过程做了多少功?
②若人停止拉绳后,至少应以多大速度立即从甲车跳到乙车才能使两车不发生碰撞?
(1)6 1.6×1014 Hz 9.1×10-8 m (2)①5.625 J ② 0.5 m/s
【解析】一群氢原子处于最高量子数为n的能级,跃迁时释放的光子种类为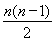 ,当n=4时,释放6种频率的光子;释放最小频率的光子时,从n=4能级跃迁到n=3能级,由E4-E3=hν,得ν=1.6×1014 Hz;要使基态的氢原子电离,需要吸收光子能量,从基态跃迁到电离态,由0-E1=
,当n=4时,释放6种频率的光子;释放最小频率的光子时,从n=4能级跃迁到n=3能级,由E4-E3=hν,得ν=1.6×1014 Hz;要使基态的氢原子电离,需要吸收光子能量,从基态跃迁到电离态,由0-E1=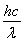 得λ=9.1×10-8 m.
得λ=9.1×10-8 m.
(2)①设甲、乙两车和人的质量分别为m甲、m乙和m人,停止拉绳时,甲车的速度为v甲,乙车的速度为v乙,由动量守恒定律得
(m甲+m人)v甲=m乙v乙
得v甲=0.25 m/s
由功与能的关系可知,人拉绳过程做的功等于系统动能的增加量.
W= (m甲+m人)v
(m甲+m人)v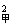 +
+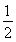 m乙v
m乙v =5.625 J.
=5.625 J.
②设人跳离甲车时人的速度为v人,人离开甲车前后由动量守恒定律得(m甲+m人)v甲=m甲v甲′+m人v人
人跳到乙车时m人v人-m乙v乙=(m人+m乙)v乙′
v甲′=v乙′
代入得v人=0.5 m/s
当人跳离甲车的速度大于或等于0.5 m/s时,两车才不会相撞.

 如图给出氢原子最低的4个能级,氢原子在这些能级之间跃迁所辐射的光子的频率最多有
如图给出氢原子最低的4个能级,氢原子在这些能级之间跃迁所辐射的光子的频率最多有 (1)某质点做匀变速直线运动,在连续两个2s内的平均速度分别是4m/s和10m/s,该质点的加速度为
(1)某质点做匀变速直线运动,在连续两个2s内的平均速度分别是4m/s和10m/s,该质点的加速度为