题目内容
7. 如图所示,在半径R=20cm、质量M=168kg的均匀铜球中,挖去一球形空穴,空穴的半径为R的一半,并且跟铜球相切,在铜球外有一质量m=1kg、体积可忽略不计的小球,这个小球位于连接铜球球心跟空穴中心的直线上,并且在空穴一边,两球心相距是d=2m,试求它们之间的相互吸引力.
如图所示,在半径R=20cm、质量M=168kg的均匀铜球中,挖去一球形空穴,空穴的半径为R的一半,并且跟铜球相切,在铜球外有一质量m=1kg、体积可忽略不计的小球,这个小球位于连接铜球球心跟空穴中心的直线上,并且在空穴一边,两球心相距是d=2m,试求它们之间的相互吸引力.
分析 用没挖之前球对质点的引力,减去被挖部分对质点的引力,就是剩余部分对质点的引力.
解答 解:万有引力公式:F=G$\frac{Mm}{{r}^{2}}$,
由其内部挖去一个半径为$\frac{1}{2}$R的球形空穴,挖去小球的质量为m′,
挖去之前的球的质量为M,则:M=8m′,
在没有挖去前,大球对小球m的万有引力:F=G$\frac{Mm}{{d}^{2}}$,
该力等效于挖去的直径为R的小球对m的力和剩余不规则部分对m的力这两个力的合力,
所以对位于球心和空穴中心边线上、与球心相距d的质点m的引力:
F′=G$\frac{Mm}{{d}^{2}}$-G$\frac{\frac{M}{8}×m}{(d-\frac{R}{2})^{2}}$=G$\frac{Mm}{{d}^{2}}$-G$\frac{Mm}{8(d-\frac{R}{2})^{2}}$=G$\frac{168×1}{{2}^{2}}$-G$\frac{168×1}{8(2-\frac{0.2}{2})^{2}}$=$\frac{13062}{361}$G≈36.18G;
答:它们之间的相互吸引力为36.18G.
点评 本题主要采用割补法的思想,根据整体球M在与小球m的引力等于割掉的小球与小球m的引力和剩余空腔部分与小球m的引力的矢量和,掌握割补思想是解决本题的主要入手点,掌握万有引力定律公式是基础.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
17.对一质量恒定的物体的运动过程,下列说法正确的是( )
| A. | 如果物体在运动过程中动量保持不变,则物体一定做匀速直线运动 | |
| B. | 若在任何相等时间内,物体所受合外力的冲量相同(不为零),则物体一定做匀变速直线运动 | |
| C. | 曲线运动一定是变速运动 | |
| D. | 曲线运动一定是变加速运动 |
18.关于楞次定律,可以理解为( )
| A. | 感应电流的磁场总是阻碍原磁场 | |
| B. | 感应电流产生的效果总是阻碍导体与磁体间的相对运动 | |
| C. | 若原磁通量增加,感应电流的磁场与原磁场同向;若原磁通量减少,感应电流的磁场跟原磁场反向 | |
| D. | 感应电流的磁场总是与原磁场反向 |
2.下列说法正确的是( )
| A. | 麦克斯韦第一次用实验验证了电磁波的存在 | |
| B. | 阳光下肥皂膜上的呈彩色条纹,是光的干涉现象 | |
| C. | 太阳光通过三棱镜产生的彩色条纹,是光的衍射现象 | |
| D. | 光的偏振说明光是横波 | |
| E. | 眼睛眯成一条线看到的发光的电灯周围有彩色花纹,是光的衍射现象 |
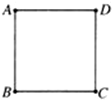 如图所示,A,B,C,D是匀强电场中一正方形的四个顶点,匀强电场方向平行与该平面.已知A,B,C三点的电势分别为φA=15V,φB=3V,φC=-3V.
如图所示,A,B,C,D是匀强电场中一正方形的四个顶点,匀强电场方向平行与该平面.已知A,B,C三点的电势分别为φA=15V,φB=3V,φC=-3V. 的成绩获得
的成绩获得 栏金牌,这里的
栏金牌,这里的 如图所示,物体在水平面上由某一初速度运动,运动s后冲上斜面,若斜面及水平面的动摩擦因数均为μ,斜面倾角为θ=37°,若物体能在斜面上上升的最大高度为H,求物体的初速度.
如图所示,物体在水平面上由某一初速度运动,运动s后冲上斜面,若斜面及水平面的动摩擦因数均为μ,斜面倾角为θ=37°,若物体能在斜面上上升的最大高度为H,求物体的初速度. 如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈abcd共100匝,线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO'匀速转动,角速度ω=2πrad/s,外电路电阻R=4Ω,求:
如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈abcd共100匝,线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO'匀速转动,角速度ω=2πrad/s,外电路电阻R=4Ω,求: