题目内容
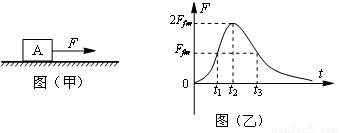
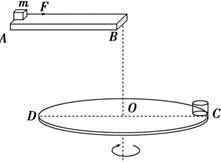
如图所示，水平放置的圆盘上，在其边缘C点固定一个小桶，桶的高度不计，圆盘半径为R＝1m，在圆盘直径CD的正上方，与CD平行放置一条水平足够长的滑道AB，滑道右端B与圆盘圆心O在同一竖直线上，且B点距离圆盘圆心的竖直高度h＝1．25 m，在滑道某处静止放置质量为m＝0．4 kg的物块（可视为质点），物块与滑道的动摩擦因数为μ＝0．2，现用力F＝4N的水平作用力拉动物块，同时圆盘从图示位置，以角速度ω＝2πrad/s，绕通过圆心O的竖直轴匀速转动，拉力作用在物块一段时间后撤掉，最终物块由B点水平抛出，恰好落入圆盘边缘的小桶内．重力加速度取10 m/s2．
（1）若拉力作用时间为0．5s，求所需滑道的长度；
（2）改变物块放置的位置，求拉力作用的最短时间。
练习册系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
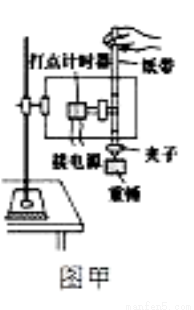
学校开展研究性学习，某同学为了探究杆子转动时的动能表达式，设计了下图甲所示的实验：质量为m的均匀长直杆一端固定在转轴O处，杆由水平位置静止释放，用置于圆弧上某位置的光电门测出另一端A经过该位置时的瞬时速度vA，并记下该位置与转轴O的高度差h．
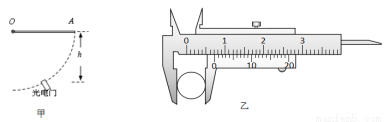
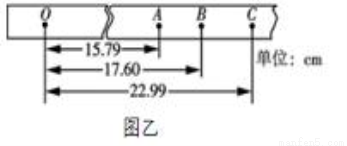
（1）该同学用20分度的游标卡尺测得长直杆的横截面的直径如图乙为 mm．
（2）调节光电门在圆弧上的位置，测得多组数据如表格所示．请选择适当的数据处理方法，猜想并写出vA与h的函数关系等式．
组次 | 1 | 2 | 3 | 4 | 5 |
h/m | 0．10 | 0．15 | 0．20 | 0．25 | 0．30 |
vA（m/s） | 1．73 | 2．12 | 2．46 | 2．74 | 3．00 |
（3）当地重力加速度g取10m/s2，不计一切摩擦，结合你找出的函数关系式，根据守恒规律写出此杆转动时动能的表达式EK= （请用数字、质量m、速度vA表示）．
