题目内容
6. 如图,质量分别为m和2m的两个小球A和B,中间用长度为2L的轻质杆相连,在杆的中点O处有一光滑的固定转动轴,把杆置于水平位置后释放,在B球摆动到最低位置时,求:
如图,质量分别为m和2m的两个小球A和B,中间用长度为2L的轻质杆相连,在杆的中点O处有一光滑的固定转动轴,把杆置于水平位置后释放,在B球摆动到最低位置时,求:(1)两球的速度大小
(2)轻杆对A球是否做功,如果做功求出做功的大小,如果不做功,说明原因.
分析 在B球顺时针摆动到最低位置的过程中,对于B球、A球和地球组成的系统机械能守恒,由于轻杆对两球做功,两球各自的机械能均不守恒,对A球根据动能定理求解杆对A做的功.
解答 解:(1)小球A、B组成的系统机械能守恒,以O点所在的水平面为零势能参考面,则有:
$\frac{1}{2}({m_A}+{m_B}){v^2}+{m_A}gL+(-{m_B}gL)=0$
解得:v=$\sqrt{\frac{2gL}{3}}$
(2)对A,根据动能定理得:
W+(-mAgL)=$\frac{1}{2}$mAv2-0
W=$\frac{4mgL}{3}$
所以轻杆对A做功.
答:(1)两球的速度大小为$\sqrt{\frac{2gL}{3}}$;
(2)轻杆对A球做功,做功的大小为$\frac{4mgL}{3}$.
点评 本题是轻杆连接的问题,要抓住单个物体机械能不守恒,而系统的机械能守恒是关键.

练习册系列答案
相关题目
16.以下关于时刻和时间间隔的说法中,不正确的是( )
| A. | “第2s末”表示一个时刻 | |
| B. | “第2s末”与“第3s初”表示同一时刻 | |
| C. | “第2s内”表示一段时间间隔 | |
| D. | “第2s内”和“2s内”表示同一时间间隔 |
17.根据电场强度的定义式E=$\frac{F}{q}$可知,电场中某一点( )
| A. | 电场强度与试探电荷受到的电场力成正比,与试探电荷的电量成反比 | |
| B. | 试探电荷的电性不同时,受到的电场力的方向不同,场强的方向也不同 | |
| C. | 试探电荷的电荷量q不同时,受到的电场力F也不同,场强也不同 | |
| D. | 电场强度由场本身决定,与是否放置试探电荷及电荷的电荷量、电性均无关 |
1. 如图所示,在水平桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力F′为( )
如图所示,在水平桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力F′为( )
 如图所示,在水平桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力F′为( )
如图所示,在水平桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力F′为( )| A. | 若桌面光滑,则F′=$\frac{MF}{M+m}$ | |
| B. | 若桌面光滑,则F′=$\frac{mF}{M+m}$ | |
| C. | 若M、m与桌面的摩擦因数均为μ,则F′=$\frac{MF}{M+m}+μMg$ | |
| D. | 若M、m与桌面的摩擦因数均为μ,则F′=$\frac{MF}{M+m}$ |
18.有一个通电长螺线管中,把一个带电粒子沿管轴线射入管中,粒子将在管中( )
| A. | 作圆周运动 | B. | 沿轴线来回运动 | ||
| C. | 作匀加速直线运动 | D. | 作匀速运动 |
16.关于功和能的关系,下列说法正确的是( )
| A. | 物体做的功越多,说明物体具有的能越多 | |
| B. | 一个物体能够做功,我们就说这个物体具有能 | |
| C. | 功是能量变化的量度,做多少功,就有多少能量发生了转化 | |
| D. | 功就是能,能就是功,二者没有区别 |

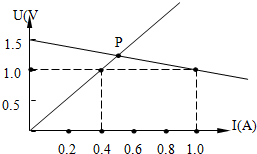 如图是某电源的U-I图象和某电阻R的U-I图象,试求:
如图是某电源的U-I图象和某电阻R的U-I图象,试求: 如图所示,竖直放置的两块足够大的带电平行板间形成一个方向水平向右的匀强电场区域,场强E=3×104N/C.在两板间用绝缘细线悬挂一个质量m=5×10-3kg的带电小球,静止时小球偏离竖直方向的夹角θ=60°.取g=10m/s2.试求:
如图所示,竖直放置的两块足够大的带电平行板间形成一个方向水平向右的匀强电场区域,场强E=3×104N/C.在两板间用绝缘细线悬挂一个质量m=5×10-3kg的带电小球,静止时小球偏离竖直方向的夹角θ=60°.取g=10m/s2.试求: