题目内容
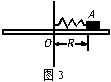
如图3所示,有一水平放置的圆盘,上面水平放一劲度系数为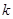 的弹簧,弹簧的一端固定于轴
的弹簧,弹簧的一端固定于轴 上,另一端连接一质量为
上,另一端连接一质量为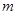 的物体A,物体与盘面间的动摩擦因数为
的物体A,物体与盘面间的动摩擦因数为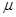 ,开始时弹簧未发生形变,长度为
,开始时弹簧未发生形变,长度为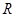 ,设最大静摩擦力等于滑动摩擦力。
,设最大静摩擦力等于滑动摩擦力。
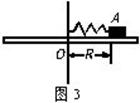
则:(1)盘的转速n0多大时,物体A开始滑动?
(2)当转速达到2n0时,弹簧的伸长量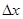 是多少?
是多少?
【答案】
(1)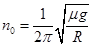 (2)
(2)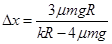
【解析】
试题分析:若圆盘转速较小,则静摩擦力提供向心力,当圆盘转速较大时,弹力与静摩擦力的合力提供向心力。
(1)当圆盘转速为n0时,A即将开始滑动,此时它所受的最大静摩擦力提供向心力,则有 ,又因为
,又因为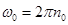 ,解得
,解得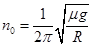 。即当
。即当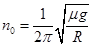 时物体A开始滑动。
时物体A开始滑动。
(2)当圆盘转速达到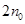 时,物体受到的最大静摩擦力已不足以提供向心力,需要弹簧的弹力来补充,即
时,物体受到的最大静摩擦力已不足以提供向心力,需要弹簧的弹力来补充,即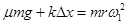 ,而
,而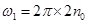 ,
,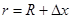 解得
解得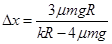
考点:考查匀速圆周运动
点评:本题难度较小,此题分析出向心力的来源是突破口,当所需的向心力大于受到的摩擦力时开始发生相对滑动,不足的向心力由弹力提供

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
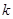 的弹簧,弹簧的一端固定于轴
的弹簧,弹簧的一端固定于轴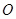 上,另一端连接一质量为
上,另一端连接一质量为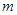 的物体A,物体与盘面间的动摩擦因数为
的物体A,物体与盘面间的动摩擦因数为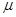 ,开始时弹簧未发生形变,长度为
,开始时弹簧未发生形变,长度为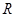 ,设最大静摩擦力等于滑动摩擦力。
,设最大静摩擦力等于滑动摩擦力。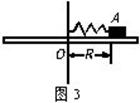
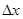 是多少?
是多少?
 B.ma
B.ma D.m(g+a)
D.m(g+a)