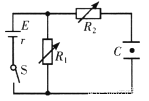
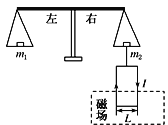
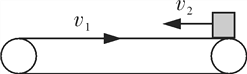
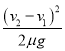ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§÷ ΝΩΈΣ1.5kgΘ§≥ΛΈΣ2.0mΒΡΡΨΑεAΖ≈‘ΎΥ°ΤΫΒΊΟφ…œΘ§ΡΨΑεA”κΒΊΟφΦδΒΡΕ·ΡΠ≤Ν“ρ ΐΈΣ0.1Θ°ΡΨΑεA…œΖ≈÷Ο÷ ΝΩΈΣ0.5kgΒΡΈοΧεBΘ§ΈοΧεBΩ…“‘Ω¥≥…÷ ΒψΘ§BΈΜ”ΎΡΨΑεA÷–Βψ¥ΠΘ§ΈοΧεA”κB÷°ΦδΒΡΕ·ΡΠ≤Ν“ρ ΐΈΣ0.1Θ§Έ 
Θ®1Θ©÷Ν…Ό”ΟΕύ¥σΥ°ΤΫΝΠά≠ΡΨΑεAΘ§≤≈Ρή ΙΡΨΑεA¥”Bœ¬≥ι≥ωΘΩ
Θ®2Θ©Β±ά≠ΝΠΈΣ7.0N ±Θ§Ψ≠ΙΐΕύ≥Λ ±ΦδAΑε¥”BΑεœ¬≥ι≥ωΘΩ¥ΥΙΐ≥Χ÷–BΑεœύΕ‘ΒΊΟφΒΡΈΜ“ΤΘΩΘ®÷ΊΝΠΦ”ΥΌΕ»g»Γ10m/s2Θ©
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚΒ±ά≠ΝΠΫœ–Γ ±Θ§AΚΆBΩ…“‘œύΕ‘Ψ≤÷Ι“ΜΤπœρ”“ΉςΦ”ΥΌ‘ΥΕ·Θ§
¥Υ ±AΓΔB÷°ΦδΖΔ…ζΒΡ «Ψ≤ΡΠ≤ΝΘ§ΗυΨί≈ΘΕΌΒΎΕΰΕ®¬…Ω…ΒΟΘ§
Ε‘’ϊΧε”–ΘΚF©¹ΠΧΘ®mA+mBΘ©g=Θ®mA+mBΘ©aΓ≠ΔΌ
ΗτάκB”–ΘΚf=mBaΓ≠ΔΎ
Β±Ψ≤ΡΠ≤ΝΝΠ¥οΒΫΉν¥σΨ≤ΡΠ≤ΝΝΠ ±Θ§ «ΝΫ’ΏΫΪΖΔ…ζœύΕ‘Μ§Ε·ΒΡΝΌΫγΉ¥Χ§Θ§
Ννf=ΠΧmBgΓ≠Δέ
ΝΣΝΔΔΌΔΎΔέ¥ζ»κ ΐΨίΩ…ΫβΒΟΘΚF=4N
¥πΘΚ÷Ν…Ό”Ο4NΒΡΥ°ΤΫΝΠά≠ΡΨΑεAΘ§≤≈Ρή ΙΡΨΑεA¥”Bœ¬≥ι≥ω
Θ®2Θ©ΫβΘΚΒ±ά≠ΝΠΈΣ7.0N ±Θ§”…≈ΘΕΌΒΎΕΰΕ®¬…ΒΟΘ§
AΈοΧεΒΡΦ”ΥΌΕ»ΈΣΘΚF©¹ΠΧΘ®mA+mBΘ©g©¹ΠΧmBg=mAaAΘ§
¥ζ»κ ΐΨίΫβΒΟΘΚaA=3m/s2Θ§
BΈοΧεΒΡΦ”ΥΌΕ»ΈΣΘΚaB=ΠΧg=0.1ΓΝ10m/s2=1m/s2Θ§
…ηΨ≠Ιΐ ±Φδt AΑε¥”BΑεœ¬≥ι≥ωΘ§‘ρΗυΨίΦΗΚΈΙΊœΒΒΟΘΚ
![]() aAt2©¹
aAt2©¹ ![]() aBt2=
aBt2= ![]() Lȧ
Lȧ
¥ζ»κ ΐΨίΫβΒΟΘΚt=1sΘ°
¥Υ ±BΑεΒΡΕ‘ΒΊΈΜ“Τ¥σ–ΓΈΣΘΚ
xB= ![]() aBt2=
aBt2= ![]() ΓΝ1ΓΝ12m=0.5mΘ§ΖΫœρœρ”“
ΓΝ1ΓΝ12m=0.5mΘ§ΖΫœρœρ”“
¥πΘΚΒ±ά≠ΝΠΈΣ7.0N ±Θ§Ψ≠Ιΐ1sΒΡ ±ΦδAΑε¥”BΑεœ¬≥ι≥ωΘΜ¥ΥΙΐ≥Χ÷–BΑεœύΕ‘ΒΊΟφΒΡΈΜ“Τ «0.5mΘ§ΖΫœρœρ”“
ΓΨΫβΈωΓΩΘ®1Θ©Β±ά≠ΝΠΫœ–Γ ±Θ§AΚΆBΩ…“‘œύΕ‘Ψ≤÷Ι“ΜΤπœρ”“ΉςΦ”ΥΌ‘ΥΕ·Θ§¥Υ ±AΓΔB÷°Φδ «Ψ≤ΡΠ≤ΝΘ§Β±Ψ≤ΡΠ≤ΝΝΠ¥οΒΫΉν¥σΨ≤ΡΠ≤ΝΝΠ ±Θ§ «ΝΫ’ΏΫΪΖΔ…ζœύΕ‘Μ§Ε·ΒΡΝΌΫγΉ¥Χ§Θ§Υυ“‘¥Υ ±ΒΡά≠ΝΠ «Ήν–Γά≠ΝΠΗυΨί≈ΘΕΌΒΎΕΰΕ®¬…Θ§‘Υ”Ο’ϊΧεΖ®ΚΆΗτάκΖ®«σ≥ω ΙΡΨΑεA¥”Bœ¬≥ι≥ω–η“Σά≠ΡΨΑεAΒΡΉν–ΓΥ°ΤΫά≠ΝΠΘΜΘ®2Θ©Β±ά≠ΝΠΈΣ7.0N ±Θ§ΗυΨί≈ΘΕΌΒΎΕΰΕ®¬…«σ≥ωΡΨΑεAΚΆΈοΧεBΒΡΦ”ΥΌΕ»Θ§ΗυΨίΈΜ“ΤΙΊœΒΦ¥Ω…«σ≥ωAΑε¥”BΑεœ¬≥ι≥ωΨ≠ΙΐΒΡ ±ΦδΘΜάϊ”ΟΈΜ“Τ ±ΦδΙΪ Ϋ«σ≥ω¥ΥΙΐ≥Χ÷–BΑεœύΕ‘ΒΊΟφΒΡΈΜ“ΤΘ°
ΓΨΩΦΒψΨΪΈωΓΩΫβ¥π¥ΥΧβΒΡΙΊΦϋ‘Ύ”ΎάμΫβΜ§Ε·ΡΠ≤ΝΝΠΒΡœύΙΊ÷Σ ΕΘ§’ΤΈ’Μ§Ε·ΡΠ≤ΝΝΠ:άϊ”ΟΙΪ Ϋf=ΠΧF N Ϋχ––ΦΤΥψΘ§Τδ÷–FN «ΈοΧεΒΡ’ΐ―ΙΝΠΘ§≤Μ“ΜΕ®Β»”ΎΈοΧεΒΡ÷ΊΝΠΘ§…θ÷ΝΩ…ΡήΚΆ÷ΊΝΠΈόΙΊ.Μρ’ΏΗυΨίΈοΧεΒΡ‘ΥΕ·Ή¥Χ§Θ§άϊ”ΟΤΫΚβΧθΦΰΜρ≈ΘΕΌΕ®¬…ά¥«σΫβΘ§“‘ΦΑΕ‘Ψ≤ΡΠ≤ΝΝΠΒΡάμΫβΘ§ΝΥΫβΨ≤ΡΠ≤ΝΝΠ:Ψ≤ΡΠ≤ΝΝΠ¥σ–ΓΩ…‘Ύ0”κfmax ÷°Φδ±δΜ·Θ§“ΜΑψ”ΠΗυΨίΈοΧεΒΡ‘ΥΕ·Ή¥Χ§”…ΤΫΚβΧθΦΰΜρ≈ΘΕΌΕ®¬…ά¥«σΫβΘ°

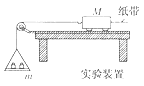
 53ΥφΧΟ≤βœΒΝ–¥πΑΗ
53ΥφΧΟ≤βœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΩΎœψΧ«ΒΡ…ζ≤ζ“―”–ΚήΨΟΒΡάζ ΖΘ°ΨΉΫάΩΎœψΧ«”–ΚήΕύ“φ¥ΠΘ§ΒΪΤδ≤–ΝτΈο“≤Μα¥χά¥Έέ»ΨΘ°ΈΣΝΥ―–ΨΩΩΎœψΧ«ΒΡ’≥ΗΫΝΠ”κΈ¬Ε»ΒΡΙΊœΒΘ§“ΜΈΜΆ§―ßΆ®Ιΐ Β―ιΘ§≤βΕ®ΝΥ≤ΜΆ§Έ¬Ε»œ¬≥ΐ»ΞΧ«Ζ÷ΒΡΩΎœψΧ«”κ¥…Ή©ΒΊΟφΒΡ’≥ΗΫΝΠΘ§ΒΟΒΫΝΥ»γ±μΥυ ΨΒΡ“ΜΉι ΐΨίΘΚ
œνΡΩ | Έ¬Ε» | ’≥ΗΫΝΠ |
1 | 15 | 2.0 |
2 | 25 | 3.1 |
3 | 30 | 3.3 |
4 | 35 | 3.6 |
5 | 37 | 4.6 |
6 | 40 | 4.0 |
7 | 45 | 2.5 |
8 | 50 | 1.4 |
Θ®1Θ©«κΗυΨί…œ ω ΐΨίΘ§‘ΎΆΦ÷–Μφ÷Τ≥ω’≥ΗΫΝΠFΥφΈ¬Ε»±δΜ·ΒΡΆΦœΏΘ°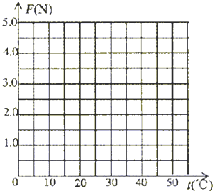
Θ®2Θ©ΗυΨί…œ ω ΐΨί“‘ΦΑΒΟΒΫΒΡΆΦœΏΘ§Ω…“‘ΒΟΒΫΒΡ Β―ιΫα¬έ «ΘΚ Θ°