题目内容
 选做题
选做题
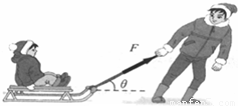
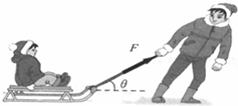
A、2009年入冬以来我市多次降雪,雪后两位同学在雪地做拉雪橇的游戏.如图所示,在水平雪地上,质量为M=35kg的小红,坐在质量为m=5kg的雪橇上,小莉用与水平方向成37°斜向上的拉力拉雪橇,拉力大小为F=100N,雪橇与地面间的动摩擦因数为μ=0.2,(sin37°=0.6,cos37°=0.8)求:
(1)雪橇对地面的压力大小;
(2)雪橇运动的加速度大小;
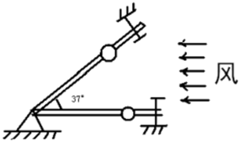
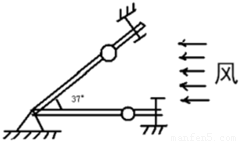
B、风洞实验室中可以产生水平方向的、大小可调节的风力,现将一套有小球的细直杆放入风洞实验室,小球孔径略大于细杆直径.如图所示.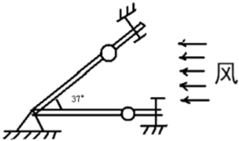
①当杆在水平方向上固定时,调节风力的大小,使小球在杆上匀速运动.这时小球所受风力为小球重力的0.5倍,试求小球与杆间的滑动摩擦因数;
②保持小球所受风力不变,使杆与水平方向间夹角为37°并固定,则小球从静止出发在细杆上滑下距离s所需的时间为多少?(sin37°=0.6,cos37°=0.8,g=10m/s2)
A:解:选小红和雪橇整体为研究对象,其受力如图所示.
(1)在y轴上由物体平衡条件得:
FN+Fsinθ=(M+m)g
解得:FN=(M+m)g-Fsinθ=340N,
由牛顿第三定律知雪橇对地面压力大小为:
FN′=FN=340N,
(2)在x轴上由牛顿第二定律得: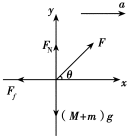
Fcosθ-Ff=(M+m)a
又由:Ff=μFN,
解得:a=0.3m/s2,
答:(1)雪橇对地面的压力大小为340N;
(2)雪橇运动的加速度大小为0.3m/s2;
B:解:①设小球受的风力为F,小球的质量为m,因小球做匀速运动,
则F=μmg,F=0.5mg,所以μ=0.5.
②对小球受力分析如图所示,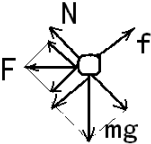
由牛顿第二定律,得
N+Fsinθ=mgcosθ
Fcosθ+mgsinθ-f=ma
又f=μN
联立以上三式可得a=0.75g
由s= at2,并代入数值,得 t=
at2,并代入数值,得 t=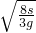 ,
,
答:①小球与杆间的滑动摩擦因数为0.5;
②小球从静止出发在细杆上滑下距离s所需的时间为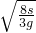 .
.
分析:A、(1)对雪橇受力分析,竖直方向上根据物体平衡条件列方程可以求得;
(2)由牛顿第二定律,可以求得物体的加速度的大小.
B、①小球在杆上匀速运动,说明受力平衡,根据平衡的条件可以求出滑动摩擦因数;
②对小球受力分析,由牛顿第二定律列方程,可以求出小球的加速度的大小,再由位移公式可以求得运动的时间.
点评:A、牛顿第二定律的直接应用,对物体受力分析后,列方程即可求出,比较简单.
B、根据小球的平衡条件求出风力的大小,当风力改变方向后,小球的受力变化,由牛顿第二定律和位移公式即可求出.
(1)在y轴上由物体平衡条件得:
FN+Fsinθ=(M+m)g
解得:FN=(M+m)g-Fsinθ=340N,
由牛顿第三定律知雪橇对地面压力大小为:
FN′=FN=340N,
(2)在x轴上由牛顿第二定律得:

Fcosθ-Ff=(M+m)a
又由:Ff=μFN,
解得:a=0.3m/s2,
答:(1)雪橇对地面的压力大小为340N;
(2)雪橇运动的加速度大小为0.3m/s2;
B:解:①设小球受的风力为F,小球的质量为m,因小球做匀速运动,
则F=μmg,F=0.5mg,所以μ=0.5.
②对小球受力分析如图所示,

由牛顿第二定律,得
N+Fsinθ=mgcosθ
Fcosθ+mgsinθ-f=ma
又f=μN
联立以上三式可得a=0.75g
由s=
 at2,并代入数值,得 t=
at2,并代入数值,得 t=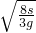 ,
,答:①小球与杆间的滑动摩擦因数为0.5;
②小球从静止出发在细杆上滑下距离s所需的时间为
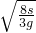 .
.分析:A、(1)对雪橇受力分析,竖直方向上根据物体平衡条件列方程可以求得;
(2)由牛顿第二定律,可以求得物体的加速度的大小.
B、①小球在杆上匀速运动,说明受力平衡,根据平衡的条件可以求出滑动摩擦因数;
②对小球受力分析,由牛顿第二定律列方程,可以求出小球的加速度的大小,再由位移公式可以求得运动的时间.
点评:A、牛顿第二定律的直接应用,对物体受力分析后,列方程即可求出,比较简单.
B、根据小球的平衡条件求出风力的大小,当风力改变方向后,小球的受力变化,由牛顿第二定律和位移公式即可求出.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
 选做题
选做题