题目内容
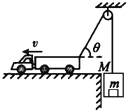
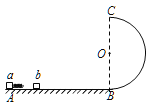
【题目】如图所示,水平光滑轨道AB与半径为R的竖直光滑半圆形轨道BC相切于B点。质量为2m和m的a、b两个小滑块(可视为质点)原来静止于水平轨道上,其中小滑块a与一轻弹簧相连。某一瞬间给小滑块a一冲量使其获得![]() 的初速度向右冲向小滑块b,与b碰撞后弹簧不与b相粘连,且小滑块b在到达B点之前已经和弹簧分离,不计一切摩擦,求:
的初速度向右冲向小滑块b,与b碰撞后弹簧不与b相粘连,且小滑块b在到达B点之前已经和弹簧分离,不计一切摩擦,求:
(1)a和b在碰撞过程中弹簧获得的最大弹性势能;
(2)小滑块b与弹簧分离时的速度;
(3)试通过计算说明小滑块b能否到达圆形轨道的最高点C。若能,求出到达C点的速度;若不能,求出滑块离开圆轨道的位置和圆心的连线与水平方向的夹角![]() 。(求出
。(求出![]() 角的任意三角函数值即可)。
角的任意三角函数值即可)。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)a与b碰撞达到共速时弹簧被压缩至最短,弹性势能最大。设此时ab的速度为v,则由系统的动量守恒可得
2mv0=3mv
由机械能守恒定律
![]()
解得:![]()
(2)当弹簧恢复原长时弹性势能为零,b开始离开弹簧,此时b的速度达到最大值,并以此速度在水平轨道上向前匀速运动。设此时a、b的速度分别为v1和v2,由动量守恒定律和机械能守恒定律可得:
2mv0=2mv1+mv2
![]()
解得: ![]()
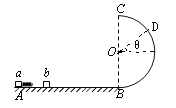
(3)设b恰能到达最高点C点,且在C点速度为vC,
由牛顿第二定律: ![]()
解得:![]()
再假设b能够到达最高点C点,且在C点速度为vC',由机械能守恒定律可得:
![]()
解得vC'=0<![]() 。所以b不可能到达C点
。所以b不可能到达C点
假设刚好到达与圆心等高处,由机械能守恒![]()
解得![]() <
<![]() 所以能越过与圆心等高处
所以能越过与圆心等高处
设到达D点时离开,如图设倾角为![]() :刚好离开有N=0,由牛顿第二定律:
:刚好离开有N=0,由牛顿第二定律:
![]()
从B到D有机械能守恒有:![]()
解得:![]()

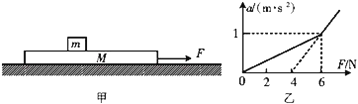
【题目】科学探究活动通常包括以下环节:提出问题、作出假设、制定计划、收集证据、评估交流等.一组同学研究“运动物体所受空气阻力与运动速度关系”的探究过程如下:
A.有同学认为:运动物体所受空气阻力可能与运动速度有关.
B.他们计划利用一些“小纸杯”作为研究对象,用超声测距仪等仪器测量“小纸杯”在空中沿直线下落时的下落距离、速度随时间变化的规律,以验证假设.
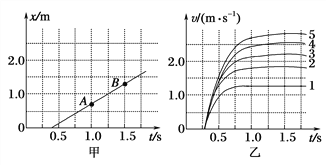
C.在相同的实验条件下,同学们首先测量了单个“小纸杯”在空中下落过程中不同时刻的下落距离,将数据填入下表中,图甲是对应的x-t图线;然后将不同数量的“小纸杯”叠放在一起从空中下落,分别测出它们的v-t图线,如图乙中图线1、2、3、4、5所示.
D.同学们对实验数据进行分析、归纳后,证实了他们的假设.
时间/s | 0.0 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 |
下落距离/m | 0.000 | 0.036 | 0.469 | 0.957 | 1.447 | x |
回答下列问题:
(1)与上述过程中A、B步骤相应的科学探究环节分别是________、________;
(2)图甲中的AB段反映了运动物体在做________运动,表中x处的值为________;
(3)图乙中各条图线具有共同特点,“小纸杯”在下落的开始阶段做________运动,最后“小纸杯”做________运动;
(4)比较图乙中的图线1和5,指出在1.0~1.5 s内,速度随时间变化关系的差异_______.