题目内容
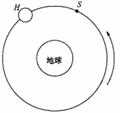
宇航员乘航天飞机去修理位于离地球表面h的圆形轨道上的哈勃太空望远镜.宇航员使航天飞机进入与太空望远镜相同的轨道.已知地球半径为R,地球表面重力加速度为g.求:
(1)在航天飞机内,一质量为m的宇航员所受的重力是多少?宇航员对航天飞机内座椅的压力是多少?
(2)航天飞机在轨道上的速率和周期是多少?
(1)在航天飞机内,一质量为m的宇航员所受的重力是多少?宇航员对航天飞机内座椅的压力是多少?
(2)航天飞机在轨道上的速率和周期是多少?
分析:(1)宇航员所受的重力等于万有引力;宇航员受到的重力提供向心力,处于完全失重状态;
(2)航天飞机在轨道上做匀速圆周运动,万有引力提供向心力,根据牛顿第二定律列式求解速率和周期.
(2)航天飞机在轨道上做匀速圆周运动,万有引力提供向心力,根据牛顿第二定律列式求解速率和周期.
解答:解:(1)宇航员所受的重力等于万有引力,为:F=G
;
地球半径为R,地球表面重力加速度为g,根据黄金代换公式GM=gR2,有:
F=
①
宇航员受到的重力提供向心力,处于完全失重状态,故对航天飞机内座椅的压力为零;
(2)航天飞机在轨道上做匀速圆周运动,万有引力提供向心力,根据牛顿第二定律,有:
F=m
②
联立①②解得:
v=
故周期为:T=
=2π
答:(1)在航天飞机内,一质量为m的宇航员所受的重力是
;宇航员对航天飞机内座椅的压力为零;
(2)航天飞机在轨道上的速率为
,周期是2π
.
| Mm |
| (R+h)2 |
地球半径为R,地球表面重力加速度为g,根据黄金代换公式GM=gR2,有:
F=
| gR2m |
| (R+h)2 |
宇航员受到的重力提供向心力,处于完全失重状态,故对航天飞机内座椅的压力为零;
(2)航天飞机在轨道上做匀速圆周运动,万有引力提供向心力,根据牛顿第二定律,有:
F=m
| v2 |
| R+h |
联立①②解得:
v=
|
故周期为:T=
| 2π(R+h) |
| v |
|
答:(1)在航天飞机内,一质量为m的宇航员所受的重力是
| gR2m |
| (R+h)2 |
(2)航天飞机在轨道上的速率为
|
|
点评:本题关键是明确航天飞机做匀速圆周运动时,万有引力提供向心力,此时宇航员处于完全失重状态.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
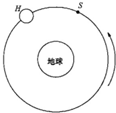 航天员乘坐航天飞机去修理位于离地球表面 h的圆形轨道上的哈勃太空望远镜片,航天飞机s进入与望远镜H相同的轨道并关闭助推火箭,而望远镜则在航天飞机前方数千米处,如图所示.设G为引力常数,M为地球质量,R为地球半径,V1为第一宇宙速度.
航天员乘坐航天飞机去修理位于离地球表面 h的圆形轨道上的哈勃太空望远镜片,航天飞机s进入与望远镜H相同的轨道并关闭助推火箭,而望远镜则在航天飞机前方数千米处,如图所示.设G为引力常数,M为地球质量,R为地球半径,V1为第一宇宙速度.