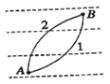
题目内容
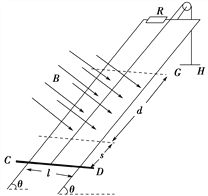
【题目】如图所示装置,电源的电动势为E=8V,内阻 r1=0.5Ω,两光滑金属导轨平行放置,间距为d=0.2m,导体棒 ab用等长绝缘细线悬挂并刚好与导轨接触,ab左侧为水平直轨道,右侧为半径R=0.2m的竖直圆弧导轨,圆心恰好为细线悬挂点,整个装置处于竖直向下的、磁感应强度为B=0.5T 的匀强磁场中。闭合开关后,导体棒沿圆弧运动,已知导体棒的质量为m=0.06kg,电阻r2=0.5Ω,不考虑运动过程中产生的反电动势,则( )
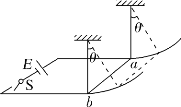
A. 导体棒ab所受的安培力方向始终与运动方向一致
B. 导体棒在摆动过程中所受安培力F=8N
C. 导体棒摆动过程中的最大动能0.8J
D. 导体棒ab速度最大时,细线与竖直方向的夹角θ=![]()
【答案】D
【解析】
A.当闭合开关S后,导体棒中电流方向始终从a到b,所受安培力方向向右,而导体棒沿圆弧摆动,故A错误;
B. 导体棒沿圆弧摆动过程中的电流
I=![]() =
=![]() A=8.0 A
A=8.0 A
导体棒受到的安培力
F=BId=0.5×8.0×0.2 N=0.8 N
故B错误;
CD.导体棒受到的重力与安培力的合力大小
F合=![]() N=1.0 N
N=1.0 N
合力与竖直方向的夹角
![]() =
=![]()
![]() =53°
=53°
故导体棒ab速度最大时,细线与竖直方向的夹角θ=53°,由动能定理,导体棒在摆动过程中的最大动能
Ekm=FR![]() -mgR(1-cos 53°)=0.08 J
-mgR(1-cos 53°)=0.08 J
故C错误,D正确。

练习册系列答案
相关题目