ƒøƒĞ»ı
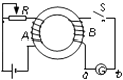
°æƒø°ø»ÁÕºÀ˘ 棨¡Ω∏˘◊„πª≥§µƒπÃ∂®∆Ω––Ω ÙµºπÏŒª”ĞÕ¨“ªÀÆ∆Ω√ʃУ¨µºπϺ‰µƒæ‡¿ÎŒ™L£¨µºπÏ…œ∫·∑≈◊≈¡Ω∏˘µºÃÂ∞Ùab∫Õcd£Æ…Ë¡Ω∏˘µºÃÂ∞Ùµƒ÷ ¡øΩ‘Œ™m£¨µÁ◊ËΩ‘Œ™R£¨µºπÏπ‚ª¨«“µÁ◊Ë≤ªº∆£¨‘Ğ’˚∏ˆµºπÏ∆Ω√ʃĞ∂º”– ˙÷±œÚ…œµƒ‘»«ø¥≈≥°£¨¥≈∏–«ø∂»Œ™B£Æø™ º ±ab∫Õcd¡ΩµºÃÂ∞Ù”–∑ΩœÚœ‡∑¥µƒÀÆ∆Ω≥ÀŸ£¨≥ÀŸ¥Û–°∑÷±Œ™V0∫Õ2V0 £¨ «Û£∫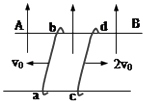
£®1£©¥”ø™ ºµΩ◊Ó÷’Œ»∂®ªÿ¬∑÷–≤˙…˙µƒΩπ∂˙»»£Æ
£®2£©µ±ab∞ٜڔ“‘À∂Ø£¨ÀŸ∂»¥Û–°±‰Œ™ ![]() ±£¨ªÿ¬∑÷–œ˚∫ƒµƒµÁ𶬠µƒ÷µ£Æ
±£¨ªÿ¬∑÷–œ˚∫ƒµƒµÁ𶬠µƒ÷µ£Æ
°æ¥∞∏°ø
£®1£©Ω‚£∫¥”ø™ ºµΩ◊Ó÷’Œ»∂®µƒπ˝≥Ã÷–£¨¡Ω∞Ù◊İ∂Ø¡ø ÿ∫„£¨‘Ú”–£∫
2mv0©Åmv0=2mv
Ω‚µ√£∫v= ![]()
”…ƒİ¡ø ÿ∫„ø…µ√¥”ø™ ºµΩ◊Ó÷’Œ»∂®ªÿ¬∑÷–≤˙…˙µƒΩπ∂˙»»Œ™£∫
Q= ![]() mv02+
mv02+ ![]() m£®2v0£©2©Å
m£®2v0£©2©Å ![]() £®2m£©v2=
£®2m£©v2= ![]() mv02
mv02
¥£∫¥”ø™ ºµΩ◊Ó÷’Œ»∂®ªÿ¬∑÷–≤˙…˙µƒΩπ∂˙»» « ![]() mv02£Æ
mv02£Æ
£®2£©Ω‚£∫µ±ab∞ÙµƒÀŸ∂»¥Û–° « ![]() «“∑ΩœÚœÚ”“ ±£¨…Ëcd∞ÙµƒÀŸ∂» «v1£¨∏˘æı∂Ø¡ø ÿ∫„µ√£∫
«“∑ΩœÚœÚ”“ ±£¨…Ëcd∞ÙµƒÀŸ∂» «v1£¨∏˘æı∂Ø¡ø ÿ∫„µ√£∫
2mv0©Åmv0=mv1+m ![]()
Ω‚µ√£∫v1= ![]()
¥À ±ªÿ¬∑÷–µƒ◊ݵÁ∂Ø ∆£∫E1=BL£® ![]() ©Å
©Å ![]() £©=
£©= ![]() BLv0
BLv0
‘Úœ˚∫ƒµƒµÁ𶬠Œ™£∫P1= ![]() =
= ![]()
¥£∫µ±ab∞ÙµƒÀŸ∂»¥Û–° « ![]() «“∑ΩœÚœÚ”“ ±£¨œ˚∫ƒµƒµÁ𶬠Œ™
«“∑ΩœÚœÚ”“ ±£¨œ˚∫ƒµƒµÁ𶬠Œ™ ![]() £Æ
£Æ
°æΩ‚Œˆ°ø”…”Ğab°¢cd¡ΩµºÃÂ∞Ù«–∏Ó¥≈∏–œş£¨ªÿ¬∑÷–≤˙…˙∏–”¶µÁ¡˜£ÆÀ¸√«‘Ğ∞≤≈‡¡¶µ√◊˜”√œ¬◊ˆºÀŸ‘À∂Ø£¨µ±abºÀŸŒ™¡„ ±£¨cd∞Ù»‘‘Мڔ“‘À∂Ø£¨“‘∫Ûcd∞ٺÖ¯ºÀŸ£¨∂¯ab∞Ù∑¥œÚº”ÀŸ£¨÷±µΩ¡Ω∞Ù¥ÔµΩπ≤Õ¨ÀŸ∂»∫Û£¨ªÿ¬∑÷–ŒŞ∏–”¶µÁ¡˜£¨¡Ω∞Ù“‘œ‡Õ¨µƒÀŸ∂»v◊ˆ‘»ÀŸ‘À∂أƣ®1£©æı¡Ω∞Ù◊İ∂Ø¡ø ÿ∫„∫Ճݡø ÿ∫„«ÛΩ‚¥”ø™ ºµΩ◊Ó÷’Œ»∂®ªÿ¬∑÷–≤˙…˙µƒΩπ∂˙»»£Æ£®2£©µ±ab∞ٜڔ“‘À∂Ø£¨ÀŸ∂»¥Û–°±‰Œ™ ![]() ±£¨∏˘æı∂Ø¡ø ÿ∫„∂®¬…∫Õ∑®¿≠µĞµÁ¥≈∏–”¶∂®¬…«ÛΩ‚£Æ
±£¨∏˘æı∂Ø¡ø ÿ∫„∂®¬…∫Õ∑®¿≠µĞµÁ¥≈∏–”¶∂®¬…«ÛΩ‚£Æ
°æøºµ„æ´Œˆ°øÕ®π˝¡ÈªÓ‘À”√∂Ø¡ø ÿ∫„∂®¬…£¨’∆Œ’∂Ø¡ø ÿ∫„∂®¬…≥…¡¢µƒÃº˛£∫œµÕ≥≤ª İÕ‚¡¶ªÚœµÕ≥À˘ İÕ‚¡¶µƒ∫œ¡¶Œ™¡„£ªœµÕ≥À˘ ݵƒÕ‚¡¶µƒ∫œ¡¶À‰≤ªŒ™¡„£¨µ´œµÕ≥Õ‚¡¶±»ƒĞ¡¶–°µ√∂‡£ªœµÕ≥À˘ İÕ‚¡¶µƒ∫œ¡¶À‰≤ªŒ™¡„£¨µ´‘Ѓ≥∏ˆ∑ΩœÚ…œµƒ∑÷¡øŒ™¡„£¨‘Ú‘Ğ∏√∑ΩœÚ…œœµÕ≥µƒ◊İ∂Ø¡øµƒ∑÷¡ø±£≥÷≤ª±‰º¥ø…“‘Ω‚¥¥À£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏