题目内容
 如图所示,两圆柱体A、B的半径均为r=0.2m,圆柱体圆心间的距离s=1.6m,在机械带动下,均以ω=8rad/s的角速度顺时针旋转,两圆柱的轴平行且在同一水平面内,均匀木板放置在两个圆柱体上面,柱面与木板间的动摩擦因数μ=0.16.开始时,木板的重心恰好在B的上方.若木板由静止开始运动,则当它的重心恰好到A的正上方时,经历的时间为(g取10m/s2)( )
如图所示,两圆柱体A、B的半径均为r=0.2m,圆柱体圆心间的距离s=1.6m,在机械带动下,均以ω=8rad/s的角速度顺时针旋转,两圆柱的轴平行且在同一水平面内,均匀木板放置在两个圆柱体上面,柱面与木板间的动摩擦因数μ=0.16.开始时,木板的重心恰好在B的上方.若木板由静止开始运动,则当它的重心恰好到A的正上方时,经历的时间为(g取10m/s2)( )| A、1s | ||
B、
| ||
| C、2s | ||
| D、1.5s |
分析:根据v=Rω求出轮子的线速度,木板在轮子上先做匀加速直线运动,当速度达到轮子的线速度时,做匀速直线运动,根据牛顿第二定律求出加速度,再根据运动学公式求出运动的时间.
解答:解:轮子的线速度为:v=Rω=0.2×8m/s=1.6m/s,木板的加速度为:a=μg=1.6m/s2,当木板达到轮子线速度所经过的位移x=
=
m=0.8m<1.6m,
知木板先做匀加速直线运动再做匀速直线运动,匀加速直线运动的时间为:t1=
=
s=1ss,
位移为0.8m,则匀速直线运动的位移为:x2=1.6-0.8m=0.8m,
匀速直线运动的时间:t2=
s=0.5ss,
所以运动的总时间为:t=t1+t2=1.5s.故D正确,A、B、C错误.
故选:D.
| v2 |
| 2a |
| 1.62 |
| 2×1.6 |
知木板先做匀加速直线运动再做匀速直线运动,匀加速直线运动的时间为:t1=
| v |
| a |
| 1.6 |
| 1.6 |
位移为0.8m,则匀速直线运动的位移为:x2=1.6-0.8m=0.8m,
匀速直线运动的时间:t2=
| 0.8 |
| 1.6 |
所以运动的总时间为:t=t1+t2=1.5s.故D正确,A、B、C错误.
故选:D.
点评:解决本题的关键能通过物体的受力判断出物体的运动情况,然后结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
 如图所示,两个相同的圆形线圈,套在光滑绝缘的水平圆柱体上,当两线圈通以方向相同的电流时,线圈的运动情况是( )
如图所示,两个相同的圆形线圈,套在光滑绝缘的水平圆柱体上,当两线圈通以方向相同的电流时,线圈的运动情况是( )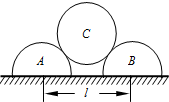 如图所示,两个截面半径均为r、质量均为m的半圆柱体A、B放在粗糙水平面上,A、B截面圆心间的距离为l.在A、B上放一个截面半径为r、质量为2m的光滑圆柱体C,A、B、C始终都处于静止状态.则( )
如图所示,两个截面半径均为r、质量均为m的半圆柱体A、B放在粗糙水平面上,A、B截面圆心间的距离为l.在A、B上放一个截面半径为r、质量为2m的光滑圆柱体C,A、B、C始终都处于静止状态.则( )
 s
s