题目内容
【题目】如图所示,长L=9 m的传送带与水平方向的倾角θ=37°,在电动机的带动下以v=4 m/s的速率沿顺时针方向运行,在传送带的B端有一离传送带很近的挡板P可将传送带上的物块挡住,在传送带的顶端A点无初速度地放一质量m=1 kg的物块,它与传送带间的动摩擦因数μ=0.5,物块与挡板碰撞的能量损失及碰撞时间不计.(g取10 m/s2,sin 37°=0.6,cos 37°=0.8) 求物体从静止释放到第一次返回上升至最高点的过程中：
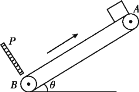
(1)系统因摩擦产生的热量；
(2)传送带多消耗的电能；
(3)物体的最终状态及该状态后电动机的输出功率．
【答案】(1)100.8 J (2)76.8J (3)16 W
【解析】
(1)物块从A点由静止释放,物块相对传送带向下滑,物块沿传送带向下加速运动的速度a1=gsin θ-μgcos θ=2 m/s2
与P碰前的速度大小v1=
=6 m/s,
物块从A到B的时间t1=
=3 s
在此过程中物块相对传送带向下的位移s1=L+vt1=21 m
物块与挡板碰撞后,以大小为v1的速度反弹,因v1>v,物块相对传送带向上滑,物块向上做减速运动的加速度大小为a2=gsin θ+μgcos θ=10 m/s2
物块速度减小到与传送带速度相等的时间t2=
=0.2 s,
在t2时间内物块向上的位移L1=
t2=1 m
此过程中物块相对传送带向上的位移s2=L1-vt2=0.2 m
物块速度与传送带速度相等后相对传送带向下滑,物块向上做减速运动的加速度大小
a3=gsin θ-μgcos θ=2 m/s2,
物块速度减小到零的时间t3=
=2 s,
在t3时间内物块向上的位移L2=
t3=4 m
此过程中物块相对传送带向下的位移s3=vt3-L2=4 m
摩擦生热Q=μmg(s1+s2+s3)cos θ=100.8 J
(2)多消耗的电能等于传送带克服摩擦力做的总功
ΔE电＝－Ff(x传送带1－x传送带2＋x传送带3)＝－μmgcosθ(vt1－vt2＋vt3)＝－76.8J
即传送带多消耗的电能为76.8J.
(3)物体返回上升到最高点时速度为零，以后将重复上述过程，且每次碰后反弹速度、上升高度依次减小，最终达到一个稳态：稳态的反弹速度大小应等于传送带速度4m/s，此后受到的摩擦力总是斜向上，加速度为a4=gsinθ－μgcosθ＝2m/s2，方向斜向下，物体相对地面做往返“类竖直上抛”运动，对地上升的最大位移为xm＝
＝4m，往返时间为T＝
＝4s；传送带受到的摩擦力大小始终为Ff＝μmgcosθ，稳态后方始终斜向下，故电动机的输出功率稳定为P＝Ffv＝μmgcosθ×v＝16W.
