题目内容
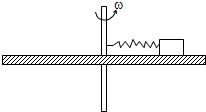如图所示，一根原长为l0=20cm的轻质弹簧，劲度系数k=40N/m，一端栓着一个质量为m=1kg的小物块，另一端固定在水平转动的转台的中心轴上．已知小物块在随转台一起做匀速圆周运动，此时弹簧的实际长度为l=25cm，小物块与转台间的动摩擦因数为μ=0.1，取g=10m/s2．求：（1）小物块运动的角速度为多大？
（2）小物块运动的周期为多大？
分析：当转台的角速度较小时，小物块有向轴心滑动的趋势；当转台的角速度较大时，小物块有远离轴心滑动的趋势． 结合牛顿第二定律求出小物块的角速度和周期．
解答：解：当转台的角速度较小时，小物块有向轴心滑动的趋势；当转台的角速度较大时，小物块有远离轴心滑动的趋势．
（1）当小物块有向轴心滑动的趋势时，其受转台的摩擦力与弹簧的拉力方向相反．设此时转台的角速度为ω1，由牛顿运动定律及圆周运动知识有
k（l-l0）-μmg=mω12l
代入数据解得ω1=2rad/s
当小物块有远离轴心滑动的趋势时，其受转台的摩擦力与弹簧的拉力方向相同．设此时转台的角速度为ω2，由牛顿运动定律及圆周运动知识有
k（l-l0）+μmg=mω22l
代入数据解得ω2=2
rad/s≈3.5rad/s
于是，转台的实际角速度为 2 rad/s≤ω≤3.5rad/s
（2）由T=
，可得转台的实际周期为8s≤T≤3.14s．
答：（1）小物块的角速度为2 rad/s≤ω≤3.5rad/s
（2）小物块的周期为8s≤T≤3.14s．
（1）当小物块有向轴心滑动的趋势时，其受转台的摩擦力与弹簧的拉力方向相反．设此时转台的角速度为ω1，由牛顿运动定律及圆周运动知识有
k（l-l0）-μmg=mω12l
代入数据解得ω1=2rad/s
当小物块有远离轴心滑动的趋势时，其受转台的摩擦力与弹簧的拉力方向相同．设此时转台的角速度为ω2，由牛顿运动定律及圆周运动知识有
k（l-l0）+μmg=mω22l
代入数据解得ω2=2
| 3 |
于是，转台的实际角速度为 2 rad/s≤ω≤3.5rad/s
（2）由T=
| 2π |
| ω |
答：（1）小物块的角速度为2 rad/s≤ω≤3.5rad/s
（2）小物块的周期为8s≤T≤3.14s．
点评：解决本题的关键理清圆周运动向心力的来源，结合牛顿第二定律进行求解．
练习册系列答案
相关题目
如图所示，一根原长为L的轻弹簧．竖直放置，下端固定在水平地面上，一个质量为m的小球，在弹簧的正上方从距地面高为H处自由下落并压缩弹簧．若弹簧的最大压缩量为x，小球下落过程受到的空气阻力恒为f，则小球下落的整个过程中，小球动能的增量为
如图所示，一根原长为L0的轻质弹簧，下端固定在水平桌面上，上端固定一个质量为m的物体A，A静止时弹簧的压缩量为△L1，在A上再放一个质量为m的物体B，待A、B静止后，再在B上施加一个竖直向下的力，力使弹簧又缩短了△L2，这时弹簧的弹性势能为EP．现突然撤去力F．求：
