题目内容
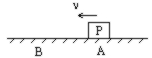
如图所示在粗糙的水平面有一个长盒A，盒的内部完全光滑，盒子长度为L，盒与水平面间的动摩擦因数μ=3/4，盒紧靠左侧有一物块B，A与B均处在某一特定场区中，场区对A、B均始终有向右的恒定作用力F=mg/2，已知盒子质量与物块的质量均为m。现同时释放A、B，此后B与A每次碰撞都是完全弹性碰撞（即每次碰撞均交换速度，且碰撞时间极短，可以忽略不计）。已知重力加速度为g。求：
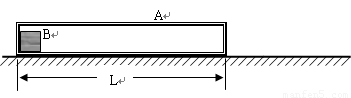
（1）物块B从开始释放到与盒A发生第一次碰撞所经过的时间t1．
（2）B与A发生第一次碰撞后，A运动的加速度大小aA和发生第二次碰撞前瞬间物块B的速度大小v2．
（3）盒A在水平面上运动的总位移大小x．
【答案】
（1）
（2）
，
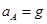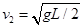（3）
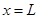
【解析】
试题分析：（1）对A而言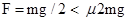
故A不动
对B而言水平方向只受到一个恒定作用力
匀加速直线运动，向右运动L后与A碰撞 
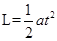
得（
(2)碰后：对A而言具有向右的初速度，但是受到水平向右的恒力和地面向左摩擦力
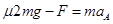
得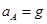
第一次B与A碰后A的速度为：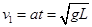
A减速为0的时间内走过的位移：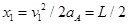
B从0再加速走过的位移：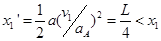
所以B加速距离
后再与A相碰：
得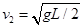
(3)B在A的左端只受到恒力作用，不可能静止，因此末状态一定是B静止在A的右端
全程应用动能定理：（整体）
得：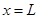
考点：动能定理 匀变速直线运动规律
练习册系列答案
一线名师权威作业本系列答案
相关题目
如图所示，粗糙的水平地面上有三块材料完全相同的木块A、B、C，质量均为m．中间用细绳l、2连接，现用一水平恒力F作用在C上，三者开始一起做匀加速运动，运动过程中把一块橡皮泥粘在某一木块上面，系统仍加速运动，则下列说法错误的是（ ）
如图所示，粗糙的水平面上放置一物体，物体在恒力F作用下做匀速直线运动，在物体发生一段位移x的过程中，求：
如图所示，粗糙的水平地面上有三块材料完全相同的木块A、B、C，质量均为m，B、C之间用轻质细绳连接．现用一水平恒力F作用在C上，三者开始一起做匀加速运动，运动过程中把一块橡皮泥粘在某一块上面，系统仍加速运动，且始终没有相对滑动．则在粘上橡皮泥并达到稳定后，下列说法正确的是（ ）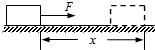
如图所示，粗糙的水平面上放置一物体，物体在恒力F作用下做匀速直线运动，在物体发生一段位移x的过程中，恒力F所做的功WF=