题目内容
 (2007?肇庆二模)如图所示,两个小球A和B质量分别是mA=2.Okg,MB=1.Okg,球A静止在光滑水平面上的M 点,球B在水平面上以初速度vo=9m/s从远处沿两球的中心连线向着球A运动.假设两球相距L≤18m时存在着F=2N的恒定斥力,L>18m时无相互作用力.求:
(2007?肇庆二模)如图所示,两个小球A和B质量分别是mA=2.Okg,MB=1.Okg,球A静止在光滑水平面上的M 点,球B在水平面上以初速度vo=9m/s从远处沿两球的中心连线向着球A运动.假设两球相距L≤18m时存在着F=2N的恒定斥力,L>18m时无相互作用力.求:(1)当两球相距最近时球A的速度;
(2)两球相距最近时的距离.
分析:(1)当两球速度相等时,两球相距最近,根据动量守恒定律求出两球相距最近时球A的速度;
(2)在两球相距L>18m时无相互作用力,两球做匀速直线运动,两球相距L≤18m时存在着F=2N的恒定斥力,做减速运动,恒力与与相对位移的乘积等于系统动能的损失.根据该功能关系求出两球相距最近时的距离.
(2)在两球相距L>18m时无相互作用力,两球做匀速直线运动,两球相距L≤18m时存在着F=2N的恒定斥力,做减速运动,恒力与与相对位移的乘积等于系统动能的损失.根据该功能关系求出两球相距最近时的距离.
解答:解:(1)两球相距最近时A球的速度与B球的速度大小相等.设速度大小为v,由动量守恒可得:
mBv0=mAv+mBv ①
代入数据解得:v=3(m/s)
(2)设两球相距最近时的距离为d,则从开始相互作用到它们之间距离最近时,它们之间的相对位移s=L-d,由动能定理可得:
Fs=
mBv02-
(mAv2+mBv2)②
代入数据解得:d=4.5(m)
答:(1)当两球相距最近时球A的速度为3m/s.
(2)两球相距最近时的距离为4.5m.
mBv0=mAv+mBv ①
代入数据解得:v=3(m/s)
(2)设两球相距最近时的距离为d,则从开始相互作用到它们之间距离最近时,它们之间的相对位移s=L-d,由动能定理可得:
Fs=
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:d=4.5(m)
答:(1)当两球相距最近时球A的速度为3m/s.
(2)两球相距最近时的距离为4.5m.
点评:本题综合考查了动量守恒定律和能量守恒定律,综合性较强,知道速度相等时,两球相距最近,以及知道恒力与与相对位移的乘积等于系统动能的损失

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 (2007?肇庆二模)某研究性学习小组,为了探索航天器球形返回舱穿过大气层时所受空气阻力(风力)的影响因素,进行了模拟实验研究.如图为测定风力的实验装置图,其中CD是一段水平放置的长为L的光滑均匀电阻丝,电阻丝电阻较大;一质量和电阻都不计的细长细长裸金属丝一端固定于O点,另一端悬挂球P,无风时细金属丝竖直,恰与电阻丝在C点接触,OC=H;有风时金属丝将偏离竖直方向,与电阻丝相交于某一点(如图中虚线所示).细金属丝与电阻丝始终保持良好的导电接触.
(2007?肇庆二模)某研究性学习小组,为了探索航天器球形返回舱穿过大气层时所受空气阻力(风力)的影响因素,进行了模拟实验研究.如图为测定风力的实验装置图,其中CD是一段水平放置的长为L的光滑均匀电阻丝,电阻丝电阻较大;一质量和电阻都不计的细长细长裸金属丝一端固定于O点,另一端悬挂球P,无风时细金属丝竖直,恰与电阻丝在C点接触,OC=H;有风时金属丝将偏离竖直方向,与电阻丝相交于某一点(如图中虚线所示).细金属丝与电阻丝始终保持良好的导电接触.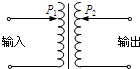 (2007?肇庆二模)如图所示,在家用交流稳压器中,变压器的原、副线圈(视作理想变压器)都带有滑动头P1、P2,当变压器输入电压发生变化时,可上下调节P1、P2的位置,使输出电压稳定在220V上,现发现输出电压低于220V,下列措施中可能使输出电压稳定在220V的是( )
(2007?肇庆二模)如图所示,在家用交流稳压器中,变压器的原、副线圈(视作理想变压器)都带有滑动头P1、P2,当变压器输入电压发生变化时,可上下调节P1、P2的位置,使输出电压稳定在220V上,现发现输出电压低于220V,下列措施中可能使输出电压稳定在220V的是( ) (2007?肇庆二模)如图(1)所示,在粗糙的水平面上,物块A在水平向右的外力F的作用下做直线运动,其v-t图象如图(2)中实线所示.下列判断正确的是( )
(2007?肇庆二模)如图(1)所示,在粗糙的水平面上,物块A在水平向右的外力F的作用下做直线运动,其v-t图象如图(2)中实线所示.下列判断正确的是( ) (2007?肇庆二模)一束红光和一束紫光以适当的角度射向向玻璃,玻璃砖为半圆形,如图所示,红光与紫光出射光线都由圆心O点沿OC方向射出,则( )
(2007?肇庆二模)一束红光和一束紫光以适当的角度射向向玻璃,玻璃砖为半圆形,如图所示,红光与紫光出射光线都由圆心O点沿OC方向射出,则( )