Question

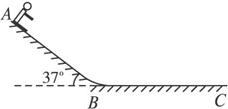
如图3-1-17所示，倾角为α=37°的足够长的斜面RQ，底端处有一固定且垂直斜面的挡板，一个小物体能沿斜面上下运动，已知小物体与斜面间的动摩擦因数μ=0.5.现使小物体以初速度v₀=10 m/s由底端Q点开始沿斜面向上运动，不计小物体与挡板每次碰撞时的能量损失，sin37°=0.6,g取10 m/s².求：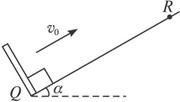

图3-1-17

（1）物体在斜面上运动时的加速度；

（2）物体第二次碰撞挡板时的速度大小和从开始运动到此时通过的路程；

（3）物体在整个运动中通过的总路程.

   

Answer 1

解析：（1）设物体向上运动的加速度大小为a_上，向下运动时加速度大小为a_下，由牛顿定律，向上时：mgsinα+μmgcosα=ma_上，向下时：mgsinα-μmgcosα=ma_下，代入数据解出a_上=10 m/s²,方向沿斜面向下；a_下=2 m/s²，方向沿斜面向下.

（2）设物体第一、二次碰挡板时的速度大小分别为v₁、v₂，由匀变速规律，在第一次上下运动中有：v₀²=2a_上s₁                                                          ①

v₁²=2a_下s₁                                                                    ②

物体在第二次上下运动中有:

v₁²=2a_上s₂                                                                    ③

v₂²=2a_下s₂                                                                    ④

解得v₂=()²·v₀=2 m/s，所求路程s=2（s₁+s₂）=12 m.

（3）由于gsinα＞μgcosα,小物体最终停在挡板上，设小物体第n次向上运动过程中路程为s_n，有s_n=s₁q^n-1,s₁=，q=,故总路程：s_总=2s_i=2=12.5［1-()ⁿ］,由于n→∞,故s_总=12.5 m.（注：本小题可用全过程动能定理，-μmgcosα·s_总=0-mv₀²，同样解得s_总=12.5 m，显得更简捷）

答案：（1）a_上=10 m/s²,a_下=2 m/s²，方向都沿斜面向下  （2）2 m/s,12 m  （3）12.5 m