题目内容
11. 如图所示,倾角θ=37°的光滑斜面固定在地面上,斜面的长度L=3.0m.质量m=0.10kg的滑块(可视为质点)从斜面顶端由静止滑下.已知sin37°=0.60,
如图所示,倾角θ=37°的光滑斜面固定在地面上,斜面的长度L=3.0m.质量m=0.10kg的滑块(可视为质点)从斜面顶端由静止滑下.已知sin37°=0.60,cos37°=0.80,空气阻力可忽略不计,重力加速度g取10m/s2.求:
(1)滑块滑到斜面底端时速度的大小;
(2)滑块滑到斜面底端时重力对物体做功的瞬时功率大小;
(3)在整个下滑过程中斜面对滑块弹力的冲量大小.
分析 (1)应用牛顿第二定律求出滑块的加速度,应用速度位移公式可以求出速度.
(2)应用功率公式求出功率.
(3)应用速度公式求出滑块的运动时间,然后根据冲量的计算公式求出冲量.
解答 解:(1)由牛顿第二定律得:mgsinθ=ma,解得:a=6m/s2,
由匀变速直线运动的速度位移公式得:v2=2aL,解得:v=6m/s;
(2)重力的瞬时功率:P=mgvcos(90°-θ),解得:P=3.6W;
(3)滑块向下滑行的时间:t=$\frac{v}{a}$=1s,
斜面对滑块弹力的冲量:I=mgcosθ•t,解得:I=0.8N•s;
答:(1)滑块滑到斜面底端时速度的大小6m/s;
(2)滑块滑到斜面底端时重力对物体做功的瞬时功率大小3.6W;
(3)在整个下滑过程中斜面对滑块弹力的冲量大小0.8N•s.
点评 本题考查了求速度、功率与冲量问题,滑块沿斜面向下做初速度为零的匀加速直线运动,应用牛顿第二定律、运动学公式、功率公式可以解题.

练习册系列答案
相关题目
2.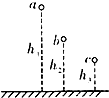 在一桌面上方有3个小球a,b,c离桌面的高度h1=30m,h2=20m,h3=10m,接先后顺序释放a,b,c,三小球刚好同时落到桌面上,不计空气阻力则有( )
在一桌面上方有3个小球a,b,c离桌面的高度h1=30m,h2=20m,h3=10m,接先后顺序释放a,b,c,三小球刚好同时落到桌面上,不计空气阻力则有( )
 在一桌面上方有3个小球a,b,c离桌面的高度h1=30m,h2=20m,h3=10m,接先后顺序释放a,b,c,三小球刚好同时落到桌面上,不计空气阻力则有( )
在一桌面上方有3个小球a,b,c离桌面的高度h1=30m,h2=20m,h3=10m,接先后顺序释放a,b,c,三小球刚好同时落到桌面上,不计空气阻力则有( )| A. | 三者到达桌面时的速度之比是3:2:1 | |
| B. | 三者运动时间之比为$\sqrt{3}$:$\sqrt{2}$:1 | |
| C. | b与a开始下落的时间差大于c与b开始下落的时间差 | |
| D. | 三者下落1s时的速度之比为1:1:1 |
6.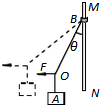 如图所示,物体A用轻质细绳与圆环B连接,圆环固定在竖直杆MN上.现用一水平力F作用在绳上的O点,将O点缓慢向左移动,使细绳与竖直方向的夹角θ逐渐增大.关于此过程,下列说法中正确的是( )
如图所示,物体A用轻质细绳与圆环B连接,圆环固定在竖直杆MN上.现用一水平力F作用在绳上的O点,将O点缓慢向左移动,使细绳与竖直方向的夹角θ逐渐增大.关于此过程,下列说法中正确的是( )
 如图所示,物体A用轻质细绳与圆环B连接,圆环固定在竖直杆MN上.现用一水平力F作用在绳上的O点,将O点缓慢向左移动,使细绳与竖直方向的夹角θ逐渐增大.关于此过程,下列说法中正确的是( )
如图所示,物体A用轻质细绳与圆环B连接,圆环固定在竖直杆MN上.现用一水平力F作用在绳上的O点,将O点缓慢向左移动,使细绳与竖直方向的夹角θ逐渐增大.关于此过程,下列说法中正确的是( )| A. | 水平力F逐渐减小 | B. | 水平力F逐渐增大 | ||
| C. | 绳对B拉力逐渐增大 | D. | A所受的合力逐渐增大 |
16.如图所示实线为电场中的电场线,虚线为带电粒子运动的轨迹( )
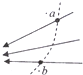

| A. | a点场强大于b点场强 | B. | a点电势高于b点电势 | ||
| C. | 可判定该粒子带负电 | D. | 不能确定该粒子带何种电 |
16.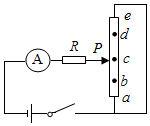 两实验小组使用相同规格的元件,按如图电路进行测量. 他们将滑动变阻器的滑片 P 分别置于 a、b、c、d、e 五个 间距相同的位置(a、e 为滑动变阻器的两个端点),把相应的电流表示数分别记录在表一、表二中.对比两组数据,发现电流表示数的变化趋势不 同.经检查,发现其中一个实验组使用的滑动变阻器发生断路.
两实验小组使用相同规格的元件,按如图电路进行测量. 他们将滑动变阻器的滑片 P 分别置于 a、b、c、d、e 五个 间距相同的位置(a、e 为滑动变阻器的两个端点),把相应的电流表示数分别记录在表一、表二中.对比两组数据,发现电流表示数的变化趋势不 同.经检查,发现其中一个实验组使用的滑动变阻器发生断路.
表一(第一实验组)
表二(第二实验组)
下列判断正确的是( )
 两实验小组使用相同规格的元件,按如图电路进行测量. 他们将滑动变阻器的滑片 P 分别置于 a、b、c、d、e 五个 间距相同的位置(a、e 为滑动变阻器的两个端点),把相应的电流表示数分别记录在表一、表二中.对比两组数据,发现电流表示数的变化趋势不 同.经检查,发现其中一个实验组使用的滑动变阻器发生断路.
两实验小组使用相同规格的元件,按如图电路进行测量. 他们将滑动变阻器的滑片 P 分别置于 a、b、c、d、e 五个 间距相同的位置(a、e 为滑动变阻器的两个端点),把相应的电流表示数分别记录在表一、表二中.对比两组数据,发现电流表示数的变化趋势不 同.经检查,发现其中一个实验组使用的滑动变阻器发生断路.表一(第一实验组)
| P 的位置 | a | b | c | d | e | |
| A 的示数(A) | 0.84 | 0.48 | 0.42 | 0.48 | 0.84 |
| P 的位置 | a | b | c | d | x | e |
| A 的示数(A) | 0.84 | 0.42 | 0.28 | 0.21 | 0.84 |
| A. | 滑动变阻器发生断路的是第二实验组 | |
| B. | 断路发生在滑动变阻器de段 | |
| C. | 表二中,对应滑片P在X(d、e 之间的某一点)处的电流表示数的可能值为0.46A | |
| D. | 表二中,对应滑片P在X(d、e 之间的某一点)处的电流表示数的可能值为0.28A |
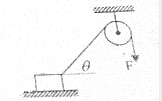 如图所示,质量为M=2kg的木块与水平地面的动摩擦因素μ=0.4,木块用轻绳绕过光滑的定滑轮,轻绳另一端施一大小为20N的恒力F,使木块沿地面向右做直线运动,定滑轮离地面的高度h=10cm,木块M可视为质点,问木块从较远处向右运动到离定滑轮多远时加速度最大?最大加速度为多少?
如图所示,质量为M=2kg的木块与水平地面的动摩擦因素μ=0.4,木块用轻绳绕过光滑的定滑轮,轻绳另一端施一大小为20N的恒力F,使木块沿地面向右做直线运动,定滑轮离地面的高度h=10cm,木块M可视为质点,问木块从较远处向右运动到离定滑轮多远时加速度最大?最大加速度为多少?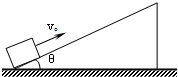
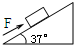 如图所示,质量为10kg的物体放在粗糙的木板上,当木板与水平面的倾角为37°时,物体恰好可以匀速下滑.(sin37°=0.6,cos37°=0.8)求:
如图所示,质量为10kg的物体放在粗糙的木板上,当木板与水平面的倾角为37°时,物体恰好可以匀速下滑.(sin37°=0.6,cos37°=0.8)求: