题目内容
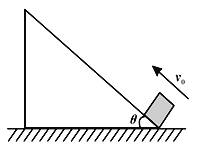
【题目】如图所示,光滑的水平面上固定一倾角为37°的粗糙斜面,紧靠斜面底端有一质量为3kg的木板,木板与斜面底端之间通过微小弧形轨道相搭接(没有连在一起,以保证滑块从斜面上滑到木板时的速度大小不变.)现有质量为1kg的滑块从斜面上高h=2.4m处由静止滑下,到达倾斜底端的速度为v0=4m/s,并以此速度滑上木板左端,最终滑块没有从木板上滑下.已知滑块与木板间的动摩擦因数μ2=0.3,取g=10m/s2 , sin37°=0.6,cos37°=0.8.求: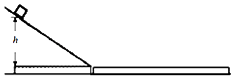
(1)斜面与滑块间的动摩擦因数μ1;
(2)滑块从滑上木板到与木板速度相同经历的时间;
(3)木板的最短长度.
【答案】
(1)解:滑块在斜面上下滑过程,
由牛顿第二定律得:mgsin 37°﹣μmgcos 37°=ma
由运动规律得: ![]()
代入数据得:μ1=0.5
答:斜面与滑块间的动摩擦因数μ1为0.5
(2)解:滑块在木板上滑动过程中,加速度大小为:
a1= ![]() =3m/s2;
=3m/s2;
木板的加速度大小为:
a2= ![]() =1m/s2
=1m/s2
设滑块从滑上木板到与木板速度相同经历的时间为t,
由题意有:v=v0﹣a1t=a2t
得:t=1s
答:滑块从滑上木板到与木板速度相同经历的时间为1s;
(3)解:由第二问求得v=1m/s
在t时间内滑块的位移为:x1= ![]() ;
;
木板的位移为:x1= ![]()
所需木板的最短长度为:Lmin=x1﹣x2
解得:Lmin=2m
答:木板的最短长度为2m.
【解析】(1)滑块从斜面下滑的过程,根据动能定理列式求解动摩擦因素;(2)(3)滑块刚好没有从木板左端滑出,说明此时它们的速度相等,由速度、位移公式可以求出木板的长度和运行的时间;
【考点精析】利用动能定理的综合应用对题目进行判断即可得到答案,需要熟知应用动能定理只考虑初、末状态,没有守恒条件的限制,也不受力的性质和物理过程的变化的影响.所以,凡涉及力和位移,而不涉及力的作用时间的动力学问题,都可以用动能定理分析和解答,而且一般都比用牛顿运动定律和机械能守恒定律简捷.