题目内容
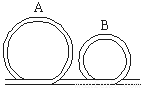
(9分)如图所示,由光滑细管组成的竖直轨道,两圆形轨道半径分别为R和R/2 ,A、B分别是两圆形轨道的最高点,质量为m的小球通过这段轨道时,在A处刚好对管壁无压力,求:

(1)小球通过A处时的速度大小;
(2)小球通过B处时的速度大小;
(3)小球在B处对管壁的压力大小。
【答案】
(1) (2)
(2) (3)
(3)
【解析】(1)在A点用牛顿第二定律:mg=m

(2)从A到B机械能守恒


(3)

由牛顿第三定律得:小球在B处对管壁的压力大小
本题考查的是圆周运动的问题。在A处刚好对管壁无压力,所以在A处只受重力作用,重力提供小球做圆周运动的向心力,由此可解出第一问;由光滑细管组成的竖直轨道,从A到B只受重力作用,机械能守恒,可以解出B点的速度;在B处受力分析可知重力和压力的合力提供小球做圆周运动的向心力,即可解出第三问。

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 如图所示,由光滑细管组成的轨道固定在竖直平面内,其中AB段和BC段是半径为R的四分之一圆弧.一小球从距离水平地面高为H的管口D处静止释放,最后能够从A点水平抛出落到地面上.若R可以变化,求:
如图所示,由光滑细管组成的轨道固定在竖直平面内,其中AB段和BC段是半径为R的四分之一圆弧.一小球从距离水平地面高为H的管口D处静止释放,最后能够从A点水平抛出落到地面上.若R可以变化,求: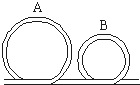 如图所示,由光滑细管组成的竖直轨道,两圆形轨道半径分别为R和
如图所示,由光滑细管组成的竖直轨道,两圆形轨道半径分别为R和 (2013?浙江模拟)如图所示,由光滑细管做成的半径R=10cm的半圆形轨道ABC(管道半径远小于轨道半径)竖直放置,A为最高点、C为最低点、B是半圆形轨道的中点且与圆心O处于同一高度.一质量m=200g的小球放在A处(在管内),小球的直径略小于管道的直径,小球与一原长L=10cm、劲度系数k=100N/m的轻弹簧相连接,弹簧的另一端固定在点O',O'点在直径AC连线上且O'C=5cm.取g=10m/s2,下列说法正确的是( )
(2013?浙江模拟)如图所示,由光滑细管做成的半径R=10cm的半圆形轨道ABC(管道半径远小于轨道半径)竖直放置,A为最高点、C为最低点、B是半圆形轨道的中点且与圆心O处于同一高度.一质量m=200g的小球放在A处(在管内),小球的直径略小于管道的直径,小球与一原长L=10cm、劲度系数k=100N/m的轻弹簧相连接,弹簧的另一端固定在点O',O'点在直径AC连线上且O'C=5cm.取g=10m/s2,下列说法正确的是( )