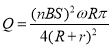题目内容
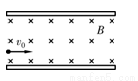
如图甲所示，质量为2kg的绝缘板静止在粗糙水平地面上，质量为1kg、边长为1m、电阻为0.1Ω的正方形金属框ABCD位于绝缘板上，E、F分别为BC、AD的中点。某时刻起在ABEF区域内有竖直向下的磁场，其磁感应强度B1的大小随时间变化的规律如图乙所示，AB边恰在磁场边缘以外；FECD区域内有竖直向上的匀强磁场，磁感应强度B2=0.5T，CD边恰在磁场边缘以内。假设金属框受到的最大静摩擦力等于滑动摩擦力，两磁场均有理想边界，取g＝10m/s2。则
A．金属框中产生的感应电动势大小为1V
B．金属框受到向左的安培力大小为1N
C．金属框中的感应电流方向沿ADCB方向
D．如果金属框与绝缘板间的动摩擦因数为0.3，则金属框可以在绝缘板上保持静止
D
【解析】
试题分析：据题意，磁感应强度B1的大小随时间变化的规律为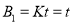
，磁感应强度B2=0.5T，在金属框内产生的电动势为：
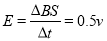，故选项A错误；金属杆受到向左的安培力为0，故选项B错误；据楞次定律可知金属框内电流方向为：ABCD，故选项C错误； 整个金属框内电流为：
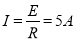,CD边受到的安培力为：
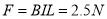,如果金属框处于静止状态，则
可以求得动摩擦因素为：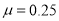
，所以当动摩擦因数为0.3时金属框处于静止状态，故选项D正确。
考点：本题考查楞次定律，法拉第电磁感应定律和物体平衡条件。
练习册系列答案
相关题目
