Question

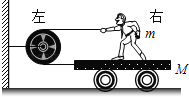
【题目】如图所示，一物块以大小v0＝8m/s的速度从足够长的传送带的底端冲上倾角θ＝37°的传送带。已知传送带顺时针转动的速度大小恒为v＝2m/s，传送带与物块间的动摩擦因数μ＝0.5，取sin37°＝0.6，cos37°＝0.8，g＝10m/s2，求：

(1)物块从开始减速到和皮带的速度相同所需的时间t1；

(2)物块沿传送带向上运动的最大距离x；

(3)物块在传送带上运动的时间t。

Answer 1

【答案】(1)1s；(2) 4m；(3)3.6s。

【解析】

(1)物块受到重力、传送带的支持力与摩擦力，选取沿传送带的方向向上为正方向，设减速过程加速度为a1、位移为s1、减速到和皮带的速度相同的时间为t1；由牛顿第二定律：

-mgsinθ-μmgcosθ=ma1

解得：

a1＝10m/s2，负号表示方向沿斜面向下；

减速到和皮带的速度相同的时间：

(2)速度相等后，由于物体所受重力沿斜面方向的分力大于滑动摩擦力，因此物体相对传送带向下运动，受到的滑动摩擦力沿斜面向上，沿斜面方向根据牛顿第二定律有：

-mgsinθ+μmgsosθ=ma2

代入数据得：

a2=-2m/s2，负号表示方向沿斜面向下；

最后减速到速度为零的时间为：

小物块向上滑行的最远距离为：

代入数据可得：

x=4m，

(3)设物块从最高点向下运动的时间为t3，该过程中物块受到的摩擦力的方向向上，所以加速度仍然是a2=-2m/s2，则：

代入数据可得：

t3=2s

所以总时间：

t=t1+t2+t3

可得：

t=3.6s。