题目内容
17.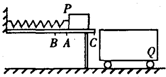 如图所示,水平放置的轻质弹簧,左端固定,右端与小物块P接触而不连接,当P到A点时,弹簧为原长,现用水平向左的推力将P缓慢地从A推到B点,需做功6J,此时在B点撤去外力后,P从表此开始沿着水平桌面滑到停放在水平光滑地面的小车Q上(小车与桌面等高).已知P的质量为m=1.0kg,Q的质量为M=4.0kg,AB的距离为5cm,AC的距离为90cm,P与桌面和Q面间的动摩擦因数均为μ=0.4.试求:
如图所示,水平放置的轻质弹簧,左端固定,右端与小物块P接触而不连接,当P到A点时,弹簧为原长,现用水平向左的推力将P缓慢地从A推到B点,需做功6J,此时在B点撤去外力后,P从表此开始沿着水平桌面滑到停放在水平光滑地面的小车Q上(小车与桌面等高).已知P的质量为m=1.0kg,Q的质量为M=4.0kg,AB的距离为5cm,AC的距离为90cm,P与桌面和Q面间的动摩擦因数均为μ=0.4.试求:(1)使P不会从Q的右端滑出,则小车至少多长?
(2)从推力作用于P到P与Q一起运动的全过程中产生的热量.
分析 (1)对从A到B再到C过程根据动能定理列式求出P的滑上小车的初速度;当P恰好不滑出小车时,两者速度相等,恰好到达小车的另一端,结合动量守恒定律和能量守恒定律求出小车的长度.
(2)根据公式Q=fS相对和能量守恒定律列式求解从推力作用于P到P与Q一起运动的全过程中产生的热量.
解答 解:(1)从A到B再到C过程,根据动能定理,有:
${W}_{F}-μmg(2{x}_{AB}+{x}_{BC})=\frac{1}{2}m{v}_{C}^{2}-0$
代入数据,解得:v=2m/s
对PQ由动量守恒定律得:mv0=(m+M)v
解得共同速度:v=$\frac{m{v}_{C}}{M+m}$=$\frac{1×2}{1+4}$m/s=0.4m/s
对PQ由功能关系得:-μmg•L=$\frac{1}{2}$(m+M)v2-$\frac{1}{2}$mvC2
代入数据解得小车最小长度:L=0.4m
(2)从推力作用于P到P与Q一起运动的全过程中产生的热量:
Q=f•((2xAB+xBC+L)=μmg•(2xAB+xBC+L)=5.6J
答:(1)使P不会从Q的右端滑出,则小车至少0.4m长;
(2)从推力作用于P到P与Q一起运动的全过程中产生的热量为5.6J.
点评 本题综合考查了动量守恒定律、能量守恒定律和动量定理,综合性较强,关键抓住临界状态,恰好不滑出时,速度相等,正好滑到小车的另一端.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
7.如图1所示,O为水平直线MN上的一点,质量为m的小球在O点的左方时受到水平恒力F1作用,运动到O点的右方时,同时还受到水平恒力F2的作用,设质点从图示位置由静止开始运动,其v-t图象如图2所示,在0-t4时间内,下列说法错误的是( )
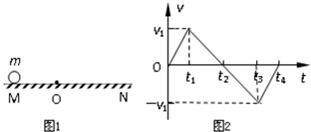

| A. | 质点在O点右方运动的时间为t4-2t1 | |
| B. | 质点在O点的左方加速度大小为$\frac{{v}_{1}}{{t}_{4}-{t}_{3}}$ | |
| C. | F2的大小为$\frac{2m{v}_{1}}{{t}_{3}-{t}_{1}}$ | |
| D. | 质点在0-t4这段时间内的最大位移为$\frac{{v}_{1}{t}_{2}}{2}$ |
12.跳高运动员从地面上跳起蹬地时( )
| A. | 地面对运动员的支持力大于运动员对地面的压力 | |
| B. | 运动员对地面的压力大于地面对运动员的支持力 | |
| C. | 地面对运动员的支持力等于运动员的重力 | |
| D. | 地面对运动员的支持力等于运动员对地面的压力 |
9.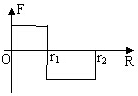 甲、乙两物体间的作用力F随它们间距r变化的情况如图所示,规定相互作用的斥力为正,引力为负.现固定甲物体,让乙物体在远处(r>r2)c以一定的初速度向甲物体运动,下列关于乙物体的运动情况描述正确的是( )
甲、乙两物体间的作用力F随它们间距r变化的情况如图所示,规定相互作用的斥力为正,引力为负.现固定甲物体,让乙物体在远处(r>r2)c以一定的初速度向甲物体运动,下列关于乙物体的运动情况描述正确的是( )
 甲、乙两物体间的作用力F随它们间距r变化的情况如图所示,规定相互作用的斥力为正,引力为负.现固定甲物体,让乙物体在远处(r>r2)c以一定的初速度向甲物体运动,下列关于乙物体的运动情况描述正确的是( )
甲、乙两物体间的作用力F随它们间距r变化的情况如图所示,规定相互作用的斥力为正,引力为负.现固定甲物体,让乙物体在远处(r>r2)c以一定的初速度向甲物体运动,下列关于乙物体的运动情况描述正确的是( )| A. | 乙物体先做匀加速运动,后做匀减速运动 | |
| B. | 乙物体先做匀减速运动,后做匀加速运动 | |
| C. | 乙物体先做匀速运动,后做匀减速运动,再做匀加速运动 | |
| D. | 乙物体先做匀速运动,后做匀加速运动,再做匀减速运动 |
1.电视机显示器接收到影像信号时,电子束从荧光屏左上角开始从左向右扫描出一条水平线,之后再扫描下一条水平线,如此高频率地从上而下扫描,使荧光屏上的亮点构成了我们看到的影像,是利用了人眼的视觉暂留效应.
2.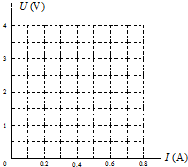 用安培表和伏特表测量电池的电动势和内电阻,得到下面的数据:
用安培表和伏特表测量电池的电动势和内电阻,得到下面的数据:
(1)在如图坐标中画出U-I关系图象.
(2)由图象可得到电动势为3V,内电阻为5Ω.
(3)(一班的答题)如果某同学把安培表接成外接法,则内电阻测量值偏小(“偏大”或“偏小”).
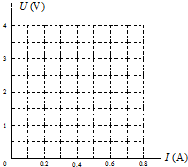 用安培表和伏特表测量电池的电动势和内电阻,得到下面的数据:
用安培表和伏特表测量电池的电动势和内电阻,得到下面的数据:| 电压U(V) | 2.5 | 2.0 | 1.5 | 1.0 | 0.5 |
| 电流I(A) | 0.1 | 0.2 | 0.29 | 0.41 | 0.51 |
(2)由图象可得到电动势为3V,内电阻为5Ω.
(3)(一班的答题)如果某同学把安培表接成外接法,则内电阻测量值偏小(“偏大”或“偏小”).
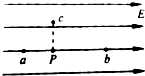 如图所示,在场强为E方向水平向右的匀强电场中,固定着一个点电荷P,a、b、c为电场中三点,其中a、b两点与点电荷P在同一水平线上,a点位于点电荷P左侧r远处,b点位于电荷P右侧2r远处,c点位于电荷P正上方r远处.若a点的场强为零,则点电荷P带有的电荷量为$\frac{E{r}^{2}}{k}$;b点场强的大小为$\frac{5E}{4}$,方向水平向右;c点场强大小为$\sqrt{2}$E,方向与水平成45°,指向右上方.
如图所示,在场强为E方向水平向右的匀强电场中,固定着一个点电荷P,a、b、c为电场中三点,其中a、b两点与点电荷P在同一水平线上,a点位于点电荷P左侧r远处,b点位于电荷P右侧2r远处,c点位于电荷P正上方r远处.若a点的场强为零,则点电荷P带有的电荷量为$\frac{E{r}^{2}}{k}$;b点场强的大小为$\frac{5E}{4}$,方向水平向右;c点场强大小为$\sqrt{2}$E,方向与水平成45°,指向右上方.