题目内容
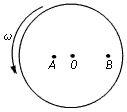
 如图所示,圆盘绕圆心O做逆时针匀速转动,圆盘上有两点A、B,OA=3cm,OB是OA的3倍,圆盘的转速n=120r/min,试求:
如图所示,圆盘绕圆心O做逆时针匀速转动,圆盘上有两点A、B,OA=3cm,OB是OA的3倍,圆盘的转速n=120r/min,试求:(1)A点转动的周期;
(2)B点转动的角速度;
(3)A、B两点转动的线速度数值.
分析:(1)周期等于转一圈所需的时间,根据转速求出A点的转动周期.
(2)根据周期,通过ω=
求出角速度的大小.
(3)A、B两点共轴转动,角速度相等,根据v=rω求出A、B两点的线速度大小.
(2)根据周期,通过ω=
| 2π |
| T |
(3)A、B两点共轴转动,角速度相等,根据v=rω求出A、B两点的线速度大小.
解答:解:(1)圆盘的转速n=120r/min,则周期T=
s=0.5s.
(2)B点转动的角速度ω=
=4πrad/s.
(3)A点的线速度vA=rAω=0.03×4π=0.12πm/s
B点的线速度vB=rBω=0.09×4π=0.36πm/s.
答:(1)A点转动的周期T=0.5s
(2)B点转动的角速度ω=4πrad/s
(3)A、B两点转动的线速度数值分别为:vA=0.12πm/s,vB=0.36πm/s.
| 60 |
| 120 |
(2)B点转动的角速度ω=
| 2π |
| T |
(3)A点的线速度vA=rAω=0.03×4π=0.12πm/s
B点的线速度vB=rBω=0.09×4π=0.36πm/s.
答:(1)A点转动的周期T=0.5s
(2)B点转动的角速度ω=4πrad/s
(3)A、B两点转动的线速度数值分别为:vA=0.12πm/s,vB=0.36πm/s.
点评:解决本题的关键掌握线速度、角速度、周期、转速之间关系,以及知道共轴转动,角速度相等.

练习册系列答案
相关题目