题目内容
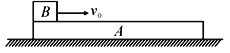
【题目】如图所示，质量为
在足够长的木板A静止在水平地面上，其上表面水平，木板A与地面间的动摩擦因数为
，一个质量为
的小物块B（可视为质点）静止于A的左端，小物块B与木板A间的动摩擦因数为
。现给小物块B一个水平向右的初速度，大小为
。求：木板A与小物块B在整个运动过程中位移大小之比（最大静摩擦力的大小等于滑动摩擦力的大小，
取
）。
【答案】
【解析】试题分别以A、B为研究对象，受力分析，木板和物块的加速度大小分别为
，
由牛顿第二定律得：
，
，
假设经过
秒A、B共速，共同速度设为
，由匀变速直线运动的规律得：
，
解得：
。
共速过程中，A的位移大小设为
，B的位移大小设为
，则
，
，
解得：
，
。
假设共速之后，A、B一起向右匀减速运动，木板和物块间的静摩擦力大小为
，木板和物块的加速度大小分别为
，由牛顿第二定律得：
，
解得：
，假设成立，
。
设共速之后至A、B均静止，A的位移设为
，B的位移设为
，则
。
整个过程中A的位移大小
，B的位移大小
则。
练习册系列答案
相关题目
