题目内容
10. 如图所示,A是地球的同步卫星.另一卫星B的圆形轨道位于赤道平面内,离地面高度为h.已知地球半径为R,地球自转角速度为ω0,地球表面的重力加速度为g,O为地球中心.
如图所示,A是地球的同步卫星.另一卫星B的圆形轨道位于赤道平面内,离地面高度为h.已知地球半径为R,地球自转角速度为ω0,地球表面的重力加速度为g,O为地球中心.(1)求卫星B的运行角速度;
(2)如卫星B绕行方向与地球自转方向相同,某时刻A、B两卫星相距最近(O、B、A在同一直线上),则至少经过多少时间,他们相距最远?
分析 (1)卫星绕地球做匀速圆周运动,根据万有引力提供向心力,列出等式表示出卫星B的运行角速度.
(2)卫星A、B绕地球做匀速圆周运动,当卫星B转过的角度与卫星A转过的角度之差等于π时,卫星再一次相距最远.
解答 解:(1)对于B卫星,由万有引力定律和向心力得
G$\frac{Mm}{(R+h)^{2}}$=m(R+h)ωB2;
在地球表面上,由m′g=G$\frac{Mm′}{{R}^{2}}$
联立解得ωB=$\sqrt{\frac{g{R}^{2}}{(R+h)^{3}}}$
(2)它们再一次相距最远时,一定是B比A多转了半圈,有:
ωBt-ω0t=π
则得 t=$\frac{π}{\sqrt{\frac{g{R}^{2}}{(R+h)^{3}}}-ω{\;}_{0}}$
答:
(1)卫星B的运行角速度为$\sqrt{\frac{g{R}^{2}}{(R+h)^{3}}}$;
(2)至少经过$\frac{π}{\sqrt{\frac{g{R}^{2}}{(R+h)^{3}}}-ω{\;}_{0}}$时间,他们相距最远.
点评 本题要求熟练应用万有引力提供向心力解决卫星的运动问题,关键要明确卫星相距最远的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.天然放射性元素放出的三种射线的穿透能力实验结果如图所示,由此可知( )


| A. | ②来自于原子核外的电子 | |
| B. | ①的电离作用最强,是一种电磁波 | |
| C. | ③的电离作用最强,是一种电磁波 | |
| D. | ③的电离作用最弱,属于原子核内释放的光子 |
5.如果运动物体有加速度,则该物体的速度大小和方向可能发生变化的是( )
| A. | 速度方向不变,大小也不变 | B. | 速度方向不变,大小改变 | ||
| C. | 速度方向改变,大小不变 | D. | 速度方向改变,大小也改变 |
15.下列关于欧姆表的说法中正确的是( )
| A. | 测量电阻时,如果待测电阻不和电源断开,可能会烧坏表头 | |
| B. | 测量电阻时,表针偏转角度越大,说明被测电阻的阻值越大 | |
| C. | 换用另一量程时,需要重新调零 | |
| D. | 测量电阻前要把红、黑表笔相接,调整调零旋钮,使指针指在电阻刻度的零位上 |
19.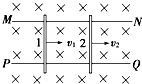 如图,在水平面上有两条平行导电导轨MN、PQ,导轨间距离为l,匀强磁场垂直于导轨所在的平面(纸面)向里,磁感应强度的大小为B,两根金属杆1、2摆在导轨上,与导轨垂直,它们分别以速度v1、v2做匀速直线运动,下列哪种情形回路中有电流通过 ( )
如图,在水平面上有两条平行导电导轨MN、PQ,导轨间距离为l,匀强磁场垂直于导轨所在的平面(纸面)向里,磁感应强度的大小为B,两根金属杆1、2摆在导轨上,与导轨垂直,它们分别以速度v1、v2做匀速直线运动,下列哪种情形回路中有电流通过 ( )
 如图,在水平面上有两条平行导电导轨MN、PQ,导轨间距离为l,匀强磁场垂直于导轨所在的平面(纸面)向里,磁感应强度的大小为B,两根金属杆1、2摆在导轨上,与导轨垂直,它们分别以速度v1、v2做匀速直线运动,下列哪种情形回路中有电流通过 ( )
如图,在水平面上有两条平行导电导轨MN、PQ,导轨间距离为l,匀强磁场垂直于导轨所在的平面(纸面)向里,磁感应强度的大小为B,两根金属杆1、2摆在导轨上,与导轨垂直,它们分别以速度v1、v2做匀速直线运动,下列哪种情形回路中有电流通过 ( )| A. | v1=v2 | B. | v1>v2 | C. | v1<v2 | D. | 以上说法都不对 |
20. 如图所示,某种洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量.设封闭空气温度不变,当洗衣缸内水位升高,则细管中被封闭的空气( )
如图所示,某种洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量.设封闭空气温度不变,当洗衣缸内水位升高,则细管中被封闭的空气( )
 如图所示,某种洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量.设封闭空气温度不变,当洗衣缸内水位升高,则细管中被封闭的空气( )
如图所示,某种洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量.设封闭空气温度不变,当洗衣缸内水位升高,则细管中被封闭的空气( )| A. | 单位体积分子数增大 | B. | 分子运动的平均动能增加 | ||
| C. | 气体一直向外界放热 | D. | 气体一直对外界做功 |
 平行板电容器AB两极板之间电压为U,间距为d.下极板与一个直径为L的半圆形金属通道相连,金属通道有两个同心的半圆形金属片CD组成,圆心贴在O′处,两个金属片彼此靠近又不接触,中间存在径向电场,即电场大小相等,方向都指向O′.半圆形通道与下极板接触点有小孔相连通.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电荷量为q的带正电微粒(微粒的重力不计),粒子在半圆形轨道间运动而不会发生碰撞.
平行板电容器AB两极板之间电压为U,间距为d.下极板与一个直径为L的半圆形金属通道相连,金属通道有两个同心的半圆形金属片CD组成,圆心贴在O′处,两个金属片彼此靠近又不接触,中间存在径向电场,即电场大小相等,方向都指向O′.半圆形通道与下极板接触点有小孔相连通.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电荷量为q的带正电微粒(微粒的重力不计),粒子在半圆形轨道间运动而不会发生碰撞. 把一根长为L=10cm的直导线垂直磁感线方向放入如图所示的匀强磁场中.
把一根长为L=10cm的直导线垂直磁感线方向放入如图所示的匀强磁场中. 一小灯泡的额定电压为6V,额定功率为1W~1.5W之间,用电流表和电压表测量它在不同电压下的电流,从而计算出它在不同电压下的实际电阻值.现有下列器材:
一小灯泡的额定电压为6V,额定功率为1W~1.5W之间,用电流表和电压表测量它在不同电压下的电流,从而计算出它在不同电压下的实际电阻值.现有下列器材: