题目内容
【题目】如图所示，A、B、C三球的质量均为m，轻质弹簧一端固定在斜面顶端、另一端与A球相连，A、B间固定一个轻杆，B、C间由一轻质细线连接．倾角为θ的光滑斜面固定在地面上，弹簧、轻杆与细线均平行于斜面，初始系统处于静止状态，细线被烧断的瞬间，下列说法正确的是（ ）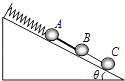
A.B球的受力情况未变，加速度为零
B.A，B两个小球的加速度均沿斜面向上，大小均为 
gsinθ
C.A，B之间杆的拉力大小为2mgsinθ
D.C球的加速度沿斜面向下，大小为2gsinθ
【答案】B
【解析】解：A、细线被烧断的瞬间，B不再受细线的拉力作用，B的受力情况发生变化，合力不为零，加速度不为零，故A错误；
B、以A、B组成的系统为研究对象，烧断细线前，A、B静止，处于平衡状态，合力为零，弹簧的弹力f=mgsinθ，烧断细线的瞬间，A、B受到的合力等于弹簧弹力，由于弹簧弹力不能突变，弹簧弹力不变，由牛顿第二定律得：mgsinθ=2ma，则加速度a= 
gsinθ，故B正确；
C、由B可知，B的加速度为：a= gsinθ，以B为研究对象，由牛顿第二定律得：T﹣mgsinθ=ma，解得：T= 
mgsinθ，故C错误；
D、对球C，由牛顿第二定律得：mgsinθ=ma，解得：a=gsinθ，方向向下，故D错误；
ACD不符合题意，B符合题意。
所以答案是：B
练习册系列答案
相关题目
