题目内容
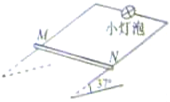 如图所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为0.5m,电阻忽略不计,其上端接一小灯泡,电阻为1Ω.一导体棒MN垂直于导轨放置,质量为0.2kg,接入电路的电阻为1Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5.在导轨间存在着垂直于导轨平面的匀强磁场,磁感应强度为0.8T.将导体棒MN由静止释放,运动一段时间后,小灯泡稳定发光,求此后导体棒MN的运动速度以及小灯泡消耗的电功率分别为是多少?(重力加速度g取10m/s2,sin37°=0.6)
如图所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为0.5m,电阻忽略不计,其上端接一小灯泡,电阻为1Ω.一导体棒MN垂直于导轨放置,质量为0.2kg,接入电路的电阻为1Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5.在导轨间存在着垂直于导轨平面的匀强磁场,磁感应强度为0.8T.将导体棒MN由静止释放,运动一段时间后,小灯泡稳定发光,求此后导体棒MN的运动速度以及小灯泡消耗的电功率分别为是多少?(重力加速度g取10m/s2,sin37°=0.6)分析:导体棒MN先向下做加速运动,后当导体棒所受合力为零时,导体棒做匀速直线运动,达到稳定状态,灯泡发光也稳定.由平衡条件可以求出导体棒MN匀速运动的速度;由E=BLv求出导体棒产生的感应电动势,然后由闭合电路欧姆定律及电功率公式求出灯泡消耗的功率.
解答:解:小灯泡稳定发光时,导体棒MN做匀速运动,所受合力为零,在沿斜面方向上,根据平衡条件得:
mgsin37°=μmgcos37°+ILB
则得:I=
又 I=
联立得:v=
=
m/s=5m/s
闭合回路的总功率为
P=
=
W=2W
小灯泡和导体棒MN的电阻相等,消耗的功率相等,则小灯泡消耗的电功率为:P灯=
P=1W
答:此后导体棒MN的运动速度为5m/s,小灯泡消耗的电功率是1W.
mgsin37°=μmgcos37°+ILB
则得:I=
| mgsin37°-μmgcos37° |
| BL |
又 I=
| BLv |
| R总 |
联立得:v=
| (mgsin37°-μmgcos37°)R总 |
| B2L2 |
| (0.2×10×0.6-0.5×0.2×10×0.8)×2 |
| 0.82×0.52 |
闭合回路的总功率为
P=
| (BLv)2 |
| R总 |
| (0.8×0.5×5)2 |
| 2 |
小灯泡和导体棒MN的电阻相等,消耗的功率相等,则小灯泡消耗的电功率为:P灯=
| 1 |
| 2 |
答:此后导体棒MN的运动速度为5m/s,小灯泡消耗的电功率是1W.
点评:本题关键抓住感应电流与安培力的关系以及与速度的关系,由平衡条件即可求出导体棒的速度,正确应用欧姆定律及电功率公式即可求出灯泡功率.

练习册系列答案
相关题目
 (2013?安徽)如图所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为0.5m,电阻忽略不计,其上端接一小灯泡,电阻为1Ω.一导体棒MN垂直于导轨放置,质量为0.2kg,接入电路的电阻为1Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5.在导轨间存在着垂直于导轨平面的匀强磁场,磁感应强度为0.8T.将导体棒MN由静止释放,运动一段时间后,小灯泡稳定发光,此后导体棒MN的运动速度以及小灯泡消耗的电功率分别为(重力加速度g取10m/s2,sin37°=0.6)( )
(2013?安徽)如图所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为0.5m,电阻忽略不计,其上端接一小灯泡,电阻为1Ω.一导体棒MN垂直于导轨放置,质量为0.2kg,接入电路的电阻为1Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5.在导轨间存在着垂直于导轨平面的匀强磁场,磁感应强度为0.8T.将导体棒MN由静止释放,运动一段时间后,小灯泡稳定发光,此后导体棒MN的运动速度以及小灯泡消耗的电功率分别为(重力加速度g取10m/s2,sin37°=0.6)( )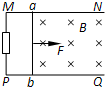 如图所示,足够长平行金属导轨MN、PQ水平放置,金属棒ab始终与导轨接触良好,导轨和金属棒的电阻不计,匀强磁场方向垂直导轨所在平面.现用垂直于棒ab的水平向右的恒力F拉ab棒由静止开始向右运动.观察某一段时间内ab棒运动速度v随时间t变化的关系哪一个是可能的( )
如图所示,足够长平行金属导轨MN、PQ水平放置,金属棒ab始终与导轨接触良好,导轨和金属棒的电阻不计,匀强磁场方向垂直导轨所在平面.现用垂直于棒ab的水平向右的恒力F拉ab棒由静止开始向右运动.观察某一段时间内ab棒运动速度v随时间t变化的关系哪一个是可能的( )
