题目内容
9.(1)行星绕太阳近似认为做匀速圆周运动,设某行星质量为m,速度为v,行星到太阳的距离为r,行星绕太阳的公转周期为T,根据开普勒第三定律、牛顿第二定律与牛顿第三定律,推导万有引力定律F=G$\frac{Mm}{{r}^{2}}$;(2)若地球半径R=6.4×106m,地球表面重力加速度g取10m/s2,试计算地球第一宇宙速度(以km/s做单位,取两位有效数字).
分析 (1)行星绕太阳能做圆周运动,是由引力提供向心力来实现的.再由开普勒第三定律可推导出万有引力定律;
(2)第一宇宙速度即为地球表面附近做圆周运动的人造卫星的运行速度,可认为其轨道半径是地球的半径R,可利用万有引力提供它做圆周运动的向心力来进行求解.
解答 解:(1)行星绕太阳做匀速圆周运动的向心力为:
$F=m\frac{{v}^{2}}{r}$
行星的线速度:v=$\frac{2πr}{v}$
由以上两式得:$F=\frac{4{π}^{2}mr}{{T}^{2}}$
不同行星的公转周期是不同的,F与r的关系式中T应消去,根据开普勒第三定律:
$\frac{{r}^{3}}{{T}^{2}}=k$
代入上式可得$F=4{π}^{2}k\frac{m}{{r}^{2}}$
说明F∝$\frac{m}{{r}^{2}}$
根据牛顿第三定律,行星对太阳的引力F′应该与太阳的质量成正比,与行星和太阳之间的距离二次方成反比,即:
F∝$\frac{Mm}{{r}^{2}}$
写成等式就是:F=$G\frac{Mm}{{r}^{2}}$
(2)卫星在地球表面上方绕地球做匀速圆周运动,根据牛顿第二定律和万有引力定律有:
$mg=m\frac{{v}^{2}}{R}$
式中R为地球半径,则v为第一宇宙速度,即$v=\sqrt{gR}=7.9km/s$
答:(1)推导见解答过程;
(2)地球的第一宇宙速度为7.9km/s.
点评 解决本题的关键能够建立正确的模型,运用牛顿第二定律、第三定律、开普勒第三定律进行推导,知道第一宇宙速度的物理意义.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
19.“轨道康复者”简称“CX”,它可在太空中给“垃圾卫星”补充能量,延长卫星的寿命,假设“CX”正在地球赤道平面内的圆周轨道上运行,运行方向与地球自转方向一致.轨道半径为地球同步卫星轨道半径的$\frac{1}{5}$,则( )
| A. | “CX”的速率是地球同步卫星速率的$\sqrt{5}$倍 | |
| B. | “CX”的加速度是地球同步卫星加速度的5倍 | |
| C. | “CX”相对于地球赤道上的观测者向西运动 | |
| D. | “CX”要实现对更低轨道上“垃圾卫星”的拯救必须直接加速 |
20. 某同学用如图所示装置做“验证机械能守恒定律”实验,在实验操作和数据处理过程中,下列做法中正确的一项是 ( )
某同学用如图所示装置做“验证机械能守恒定律”实验,在实验操作和数据处理过程中,下列做法中正确的一项是 ( )
 某同学用如图所示装置做“验证机械能守恒定律”实验,在实验操作和数据处理过程中,下列做法中正确的一项是 ( )
某同学用如图所示装置做“验证机械能守恒定律”实验,在实验操作和数据处理过程中,下列做法中正确的一项是 ( )| A. | 必须用天平称出重物的质量 | |
| B. | 必须先接通电源再释放纸带 | |
| C. | 必须选择打第1个点与第2个点的间隔约为2mm的纸带 | |
| D. | 为减小长度测量的误差,处理纸带时必须每五个计时点取一个计数点 |
4.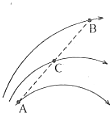 如图所示是某电场中的三条电场线,C点时A、B连线的中点.已知A点的电势是φA=30V,B点的电势φB=-20V,则下列说法正确的是( )
如图所示是某电场中的三条电场线,C点时A、B连线的中点.已知A点的电势是φA=30V,B点的电势φB=-20V,则下列说法正确的是( )
 如图所示是某电场中的三条电场线,C点时A、B连线的中点.已知A点的电势是φA=30V,B点的电势φB=-20V,则下列说法正确的是( )
如图所示是某电场中的三条电场线,C点时A、B连线的中点.已知A点的电势是φA=30V,B点的电势φB=-20V,则下列说法正确的是( )| A. | C点的电势φC=5V | |
| B. | C点的电势φC>5V | |
| C. | C点的电势φC<5V | |
| D. | 负电荷在A点的电势能大于在B点的电势能 |
1.新型火星探测器“好奇号”经过八个半月的旅行着陆火星表面,已知“好奇号”质量为M,在火星表面附近竖直下降速度为v0时,启动火箭引擎产生推力F,经过时间t,减速为零恰好安全着陆,若火星的半径为R,结合以上信息,则在火星表面发射一颗环绕卫星,它的最小发射速度应为( )
| A. | $\sqrt{(\frac{F}{M}-\frac{{v}_{0}}{t})R}$ | B. | $\sqrt{(\frac{F}{M}+\frac{{v}_{0}}{t})R}$ | C. | $\frac{FtR}{M{v}_{0}}$ | D. | $\frac{F{v}_{0}R}{Mt}$ |
18.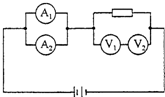 如图所示,四个相同的电流表分别改装成两个安培表和两个伏特表,安培表A1的量程大于A2的量程,伏特表V1的量程大于V2的量程,把它们按图接入电路中,则下列说法正确的是( )
如图所示,四个相同的电流表分别改装成两个安培表和两个伏特表,安培表A1的量程大于A2的量程,伏特表V1的量程大于V2的量程,把它们按图接入电路中,则下列说法正确的是( )
 如图所示,四个相同的电流表分别改装成两个安培表和两个伏特表,安培表A1的量程大于A2的量程,伏特表V1的量程大于V2的量程,把它们按图接入电路中,则下列说法正确的是( )
如图所示,四个相同的电流表分别改装成两个安培表和两个伏特表,安培表A1的量程大于A2的量程,伏特表V1的量程大于V2的量程,把它们按图接入电路中,则下列说法正确的是( )| A. | 安培表A1的读数大于安培表A2的读数 | |
| B. | 安培表A1的偏转角大于安培表A2的偏转角 | |
| C. | 伏特表V1的读数小于伏特表V2的读数 | |
| D. | 伏特表V1的偏转角等于伏特表V2的偏转角 |
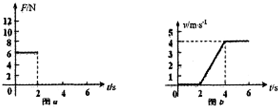 一质量为m=2kg的物块放置在粗糙的水平地面上,受到一个随时间变化的水平拉力F作用,F在0-2s内的图象如图a所示,物块的速度v随时间t变化的关系如图b所示.已知物块与水平地面间的动摩擦因数μ=0.4,g=10m/s2.
一质量为m=2kg的物块放置在粗糙的水平地面上,受到一个随时间变化的水平拉力F作用,F在0-2s内的图象如图a所示,物块的速度v随时间t变化的关系如图b所示.已知物块与水平地面间的动摩擦因数μ=0.4,g=10m/s2. 如图甲所示,一定质量的理想气体被活塞封闭在竖直放置的柱形气缸内,活塞与气缸壁无摩擦且不漏气.已知活塞横截面积S=10cm2,外界大气压p0=1.00×105Pa,初始时刻(图中A点)活塞稳定时缸内气体温度为27℃、压强为p1=1.05×105Pa.现使缸内气体温度缓慢升高,其压强随着温度变化的p-t图象如图乙所示.图象中B点时刻所对应缸内气体的体积是初始时的$\frac{7}{6}$倍,重力加速度g取10m/s2.求:
如图甲所示,一定质量的理想气体被活塞封闭在竖直放置的柱形气缸内,活塞与气缸壁无摩擦且不漏气.已知活塞横截面积S=10cm2,外界大气压p0=1.00×105Pa,初始时刻(图中A点)活塞稳定时缸内气体温度为27℃、压强为p1=1.05×105Pa.现使缸内气体温度缓慢升高,其压强随着温度变化的p-t图象如图乙所示.图象中B点时刻所对应缸内气体的体积是初始时的$\frac{7}{6}$倍,重力加速度g取10m/s2.求: