如下图甲所示.足够长的光滑平行金属导轨MN.PQ固定在同一水平面上.两导轨间距L=0.30 m.导轨电阻忽略不计.其间连接有定值电阻R=0.40 Ω.导轨上静置一质量m=0.10 kg.电阻r=0.20 Ω的金属杆ab.整个装置处于磁感应强度B=0.50 T的匀强磁场中.磁场方向竖直向下.用一外力F沿水平方向拉金属杆ab.使它由静止开始运动(金属杆与导题目和参考答案——青夏教育精英家教网—

题目内容

如下图甲所示，足够长的光滑平行金属导轨MN、PQ固定在同一水平面上，两导轨间距L=0.30 m。导轨电阻忽略不计，其间连接有定值电阻R=0.40 Ω。导轨上静置一质量m=0.10 kg、电阻r=0.20 Ω的金属杆ab，整个装置处于磁感应强度B=0.50 T的匀强磁场中，磁场方向竖直向下。用一外力F沿水平方向拉金属杆ab，使它由静止开始运动（金属杆与导轨接触良好并保持与导轨垂直），电流传感器（不计传感器的电阻）可将通过R的电流I即时采集并输入计算机，获得电流I随时间t变化的关系如图乙所示。求金属杆开始运动2.0 s时：

甲乙

（1）金属杆ab受到安培力的大小和方向；

（2）金属杆的速率；

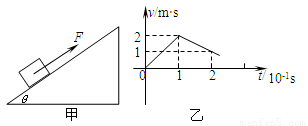
（3）对图象分析表明，金属杆在外力作用下做的是匀加速运动，加速度大小a=0.40 m/s²，计算2.0 s时外力F做功的功率。

解：（1）由图乙可知2.0 s时通过金属杆ab的电流为0.2 A,

设此时金属杆受到的安培力为F_安，根据安培力公式有

F_安=BIL

解得：F_安=3.0×10^-2 N

方向水平向左.

（2）设金属杆产生的感应电动势为E，根据闭合电路欧姆定律

解得：E=0.12 V

设金属杆在2.0 s时的速率为v₁，则

E=BLv₁

解得：v₁=0.80 m/s.

(3)根据牛顿第二定律

F-F_安=ma

解得：在2.0 s时拉力F=7.0×10^-2 N

设2.0 s时拉力F做功的功率为P，则P=Fv₁

解得：P=5.6×10^-2 W.

练习册系列答案

线圈的匝数较多（选填“A”或“B”）．
（2）如果把它看做理想变压器，现要测量A线圈的匝数，提供的器材有：一根足够长绝缘导线、一只多用电表和低压交流电源，请完成实验的步骤填空：①用绝缘导线在线圈的外部或变压器的铁芯上绕制n匝线圈；
②将

线圈与低压交流电源相连接；
③用多用电表的

交流电压

挡分别测量A线圈的输入电压U_A和绕制线圈的输出电压U
④则A线圈的匝数为

．

【2012•山东模拟】如下图甲所示，两足够长平行光滑的金属导轨MN、PQ相距为L，导轨平面与水平面夹角α，导轨电阻不计。匀强磁场垂直导轨平面向上，长为L的金属棒ab垂直于MN、PQ放置在导轨上，且始终与导轨电接触良好，金属棒的质量为m、电阻为R，另有一条纸带固定金属棒ab上，纸带另一端通过打点计时器（图中未画出），且能正常工作。在两金属导轨的上端连接右端电路，灯泡的电阻R_L=4R，定值电阻R₁=2R，电阻箱电阻调到使R₂=12R，重力加速度为g，现将金属棒由静止释放，同时接通打点计时器的电源，打出一条清晰的纸带，已知相邻点迹的时间间隔为T，如下图乙所示，试求：

（1）求磁感应强度为B有多大？

（2）当金属棒下滑距离为S₀时速度恰达到最大，求金属棒由静止开始下滑2S₀的过程中，整个电路产生的电热。

如下图甲所示，两足够长平行光滑的金属导轨MN、PQ相距为L，导轨平面与水平面夹角α，导轨电阻不计。匀强磁场垂直导轨平面向上，长为L的金属棒ab垂直于MN、PQ放置在导轨上，且始终与导轨电接触良好，金属棒的质量为m、电阻为R，另有一条纸带固定金属棒ab上，纸带另一端通过打点计时器（图中未画出），且能正常工作。在两金属导轨的上端连接右端电路，灯泡的电阻R_L=4R，定值电阻R₁=2R，电阻箱电阻调到使R₂=12R，重力加速度为g，现将金属棒由静止释放，同时接通打点计时器的电源，打出一条清晰的纸带，已知相邻点迹的时间间隔为T，如下图乙所示，试求：

1.求磁感应强度为B有多大？

2.当金属棒下滑距离为S₀时速度恰达到最大，求金属棒由静止开始下滑2S₀的过程中，整个电路产生的电热。

如下图甲所示，质量为m＝1kg的物体置于倾角为θ＝37°固定斜面(足够长)上，对物体施以平行于斜面向上的拉力F，t1＝1s时撤去拉力，物体运动的部分 —t图像如图乙，试求：(g=10m/s2)

（1）物体沿斜面上行时加速运动与减速运动的加速度大小；

（2）物体与斜面间的滑动摩擦因数μ；

（3）第1s内拉力F的平均功率

试题分类