题目内容
19.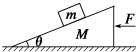 如图所示,质量为m=1kg的物块放在倾角为θ=37°的斜面体上,斜面质量为M=2kg,斜面与物块间的动摩擦因数为μ=0.2,地面光滑,现对斜面体施一水平推力F,要使物体m相对斜面静止,试确定推力F的取值范围.
如图所示,质量为m=1kg的物块放在倾角为θ=37°的斜面体上,斜面质量为M=2kg,斜面与物块间的动摩擦因数为μ=0.2,地面光滑,现对斜面体施一水平推力F,要使物体m相对斜面静止,试确定推力F的取值范围.
分析 用极限法把F推向两个极端来分析:当F较小(趋近于0)时,由于μ<tanθ,因此物块将沿斜面加速下滑;若F较大(足够大)时,物块将相对斜面向上滑,因此F不能太小,也不能太大,根据牛顿第二定律,运用整体隔离法求出F的取值范围.
解答 解:(1)设物块处于相对斜面向下滑动的临界状态时的推力为F1,此时物块受力如下图所示,取加速度的方向为x轴正方向: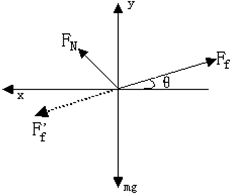
对物块分析,在水平方向有FNsinθ-μFNcosθ=ma1,
竖直方向有FNcosθ+μFNsinθ-mg=0,
对整体有F1=(M+m)a1,
代入数值得${a}_{1}=4.78m/{s}^{2}$,F1=14.35N.
(2)设物块处于相对斜面向上滑动的临界状态时的推力为F2,对物块受力分析,
在水平方向有FNsinθ+μFNcosθ=ma2,
竖直方向有FNcosθ-μFNsinθ-mg=0,
对整体有F2=(M+m)a2,
代入数值得${a}_{2}=11.18m/{s}^{2}$,F2=33.53N
综上所述可知推力F的取值范围为:14.25N≤F≤33.53N.
答:推力F的取值范围为14.25N≤F≤33.53N.
点评 解决本题的关键能够正确地受力分析,抓住临界状态,运用牛顿第二定律进行求解,注意整体法和隔离法的运用.

练习册系列答案
相关题目
19.一质点从t=0开始沿x轴做直线运动,其位置坐标与时间的关系为x=2t3-8t+1(x和t的单位分别为m和s),则下列说法中正确的是( )
| A. | 质点一直向x轴正方向运动 | |
| B. | 质点做匀变速直线运动 | |
| C. | 质点在第2s内的平均速度大小为6m/s | |
| D. | 质点在前2s内的位移为零 |
10.如图是蹦床运动员落在弹簧床面的示意图,忽略空气阻力,下面说法正确的是( )


| A. | 运动员下落到刚接触蹦床时,速度最大 | |
| B. | 运动到最低点时,床对运动员的作用力大于运动员对床的作用力 | |
| C. | 从刚接触蹦床到运动至最低点的过程中,运动员一直处于超重状态,运动员的加速度先减小后增大 | |
| D. | 在下落过程中,重力对运动员所做的功等于其重力势能的减小 |
14.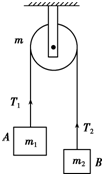 如图所示,一不可伸长的轻质细绳跨过定滑轮后,两端分别悬挂质量为m1和m2的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的磨擦.设细绳对A和B的拉力大小分别为T1和T2,已知下列四个,关于T1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析,判断正确的表达式是( )
如图所示,一不可伸长的轻质细绳跨过定滑轮后,两端分别悬挂质量为m1和m2的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的磨擦.设细绳对A和B的拉力大小分别为T1和T2,已知下列四个,关于T1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析,判断正确的表达式是( )
 如图所示,一不可伸长的轻质细绳跨过定滑轮后,两端分别悬挂质量为m1和m2的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的磨擦.设细绳对A和B的拉力大小分别为T1和T2,已知下列四个,关于T1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析,判断正确的表达式是( )
如图所示,一不可伸长的轻质细绳跨过定滑轮后,两端分别悬挂质量为m1和m2的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的磨擦.设细绳对A和B的拉力大小分别为T1和T2,已知下列四个,关于T1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析,判断正确的表达式是( )| A. | T1=$\frac{(m+2{m}_{2}){m}_{1}g}{m+2({m}_{1}+{m}_{2})}$ | B. | T1=$\frac{(m+2{m}_{1}){m}_{1}g}{m+4({m}_{1}+{m}_{2})}$ | ||
| C. | T1=$\frac{(m+4{m}_{2}){m}_{1}g}{m+2({m}_{1}+{m}_{2})}$ | D. | T1=$\frac{(m+4{m}_{1}){m}_{2}g}{m+4({m}_{1}+{m}_{2})}$ |
8. 一列横波沿x轴传播,如图所示,t1时刻的波形图为实线,t2时刻的波形图为虚线,已知t2=t1+0.375s,振动周期为0.5s,则波的传播方向和传播距离是( )
一列横波沿x轴传播,如图所示,t1时刻的波形图为实线,t2时刻的波形图为虚线,已知t2=t1+0.375s,振动周期为0.5s,则波的传播方向和传播距离是( )
 一列横波沿x轴传播,如图所示,t1时刻的波形图为实线,t2时刻的波形图为虚线,已知t2=t1+0.375s,振动周期为0.5s,则波的传播方向和传播距离是( )
一列横波沿x轴传播,如图所示,t1时刻的波形图为实线,t2时刻的波形图为虚线,已知t2=t1+0.375s,振动周期为0.5s,则波的传播方向和传播距离是( )| A. | 沿x轴正方向,9m | B. | 沿x轴负方向,3m | C. | 沿x轴正方向,3m | D. | 沿x轴负方向,9m |
